一维最优化方法

目录

• • 1. 区间搜索
  • 2. 黄金分割法
    • 2.1 区间消去
    • 2.2 黄金分割法原理
  • 3. 如何使用
    • 3.1 创建项目
    • 3.2 构建、运行

包含区间搜索以及黄金分割法的介绍

作者

赵曦

日期

2024/05/06

版本

1.0

上一篇教程：自动求导、数值微分 ↑
下一篇教程：多维无约束最优化方法 ↓

---

\[ \def\red#1{\color{red}{#1}} \def\teal#1{\color{teal}{#1}} \def\green#1{\color{green}{#1}} \def\transparent#1{\color{transparent}{#1}} \def\orange#1{\color{orange}{#1}} \def\fml#1{\text{(#1)}} \]

1. 区间搜索

在使用一维优化方法搜索目标函数的极小值点时，首先要确定搜索区间 \([a,b]\)，这个搜索区间要包含目标函数的极小值点，而且是单峰区间，即在这个区间内，目标函数只有一个极小值点。

在单峰区间内，函数值具有“高—低—高”的特点。根据这一特点，可以采用进退法来找到搜索区间。

进退法分为

• 初始探察确定进退
• 前进或者后退寻查

两步，其步骤如下

图 1 进退法

1. 选择一个初始点 \(\alpha_1\)和一个初始步长 \(h\)。
2. 如图 1(a) 所示，计算点 \(\alpha_1\)和点 \(\alpha_1+h\)对应的函数值 \(f(\alpha_1)\)和 \(f(\alpha_1+h)\)，令

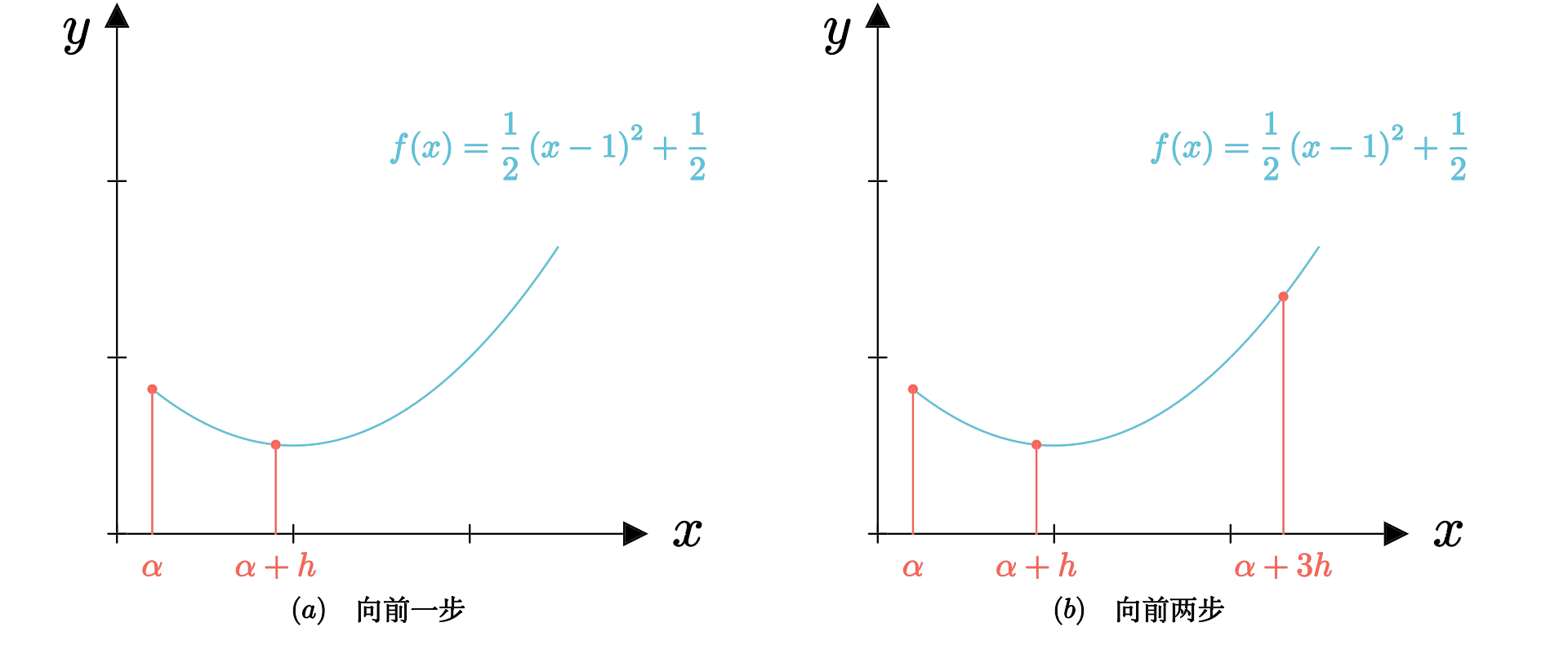
   \[f_1=f(\alpha_1),\quad f_2=f(\alpha_1+h)\]

3. 比较 \(f_1\)和 \(f_2\)，若 \(f_1>f_2\)，则执行前进运算，将步长加大 \(k\)倍（如加大 2 倍），取新点 \(\alpha_1+3h\)，如图 1(b) 所示，计算其函数值，并令

   \[f_1=f(\alpha_1+h),\quad f_2=f(\alpha_1+3h)\]

   若 \(f_1< f_2\)，则初始搜索区间端点为

   \[a=\alpha_1,\quad b=\alpha_1+3h\]

   若 \(f_1=f_2\)，则初始搜索区间端点为

   \[a=\alpha_1+h,\quad b=\alpha_1+3h\]

   若 \(f_1>f_2\)，则要继续做前进运算，且步长再加大两倍，取第 4 个点 \(\alpha_1+7h\)，再比较第 3 和第 4 个点处的函数值……如此反复循环，直到在连续的 3 个点的函数值出现“两头大、中间小”的情况为止。
4. 如果在 步骤 3 中出现 \(f_1< f_2\)的情况，则执行后退运算，将步长变为负值，取新点 \(\alpha_1-h\)，计算函数值，令

   \[f_1=f(\alpha_1-h),\quad f_2=f(\alpha_1)\]

   若 \(f_1>f_2\)，则初始搜索区间端点为

   \[a=\alpha_1-h,\quad b=\alpha_1+h\]

   若 \(f_1=f_2\)，则初始搜索区间端点为

   \[a=\alpha_1-h,\quad b=\alpha_1\]

   若 \(f_1< f_2\)，则要继续做后退运算，且步长再加大两倍，取第 4 个点 \(\alpha_1-3h\)，再比较第 3 和第 4 个点处的函数值……如此反复循环，直到在连续的 3 个点的函数值出现“两头大、中间小”的情况为止。

示例

试用进退法确定目标函数 \(f(\alpha)=\alpha^2-5\alpha+8\)的一维优化初始搜索区间 \([a,b]\)。设初始点 \(\alpha_1=0\)，初始步长 \(h=1\)

解： 由初始点 \(\alpha_1=0\)，初始步长 \(h=1\)，得

\[f_1=f(\alpha_1)=8,\quad f_2=f(\alpha_1+h)=4\]

因为 \(f_1>f_2\)，所以执行前进运算，将步长加大 2 倍，取新点 \(\alpha_1+3h=3\)，令

\[f_1=f(\alpha_1+h)=4,\quad f_2=f(\alpha_1+3h)=2\]

因为 \(f_1>f_2\)，应继续做前进运算，且步长再加大 2 倍，取第 4 个点 \(\alpha_1+7h=7\)。令

\[f_1=f(\alpha_1+3h)=2,\quad f_2=f(\alpha_1+7h)=22\]

此时 \(f_1< f_2\)，在连续的 3 个点 \(\alpha_1+h\)， \(\alpha_1+3h\)， \(\alpha_1+7h\)的函数值出现了“两头大、中间小”的情况，则初始搜索区间端点为

\[a=\alpha_1+h=1,\quad b=\alpha_1+7h=7\]

2. 黄金分割法

2.1 区间消去

黄金分割法是利用区间消去法的原理，通过不断缩小单峰区间长度，即每次迭代都消去一部分不含极小值点的区间，使搜索区间不断缩小，从而逐渐逼近目标函数极小值点的一种优化方法。黄金分割法是直接寻优法，通过直接比较区间上点的函数值的大小来判断区间的取舍。这种方法具有计算简单、收敛速度快等优点。

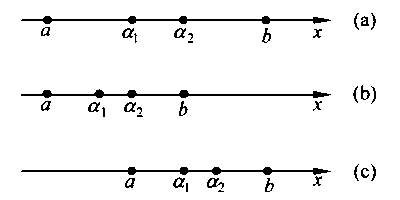
如图 1(b) 所示，在已确定的单峰区间[a,b]内任取 \(\alpha_1\)， \(\alpha_2\)两点，计算并比较两点处的函数值 \(f(\alpha_1)\)和 \(f(\alpha_2)\),可能出现3种情况：

1. \(f(\alpha_1)< f(\alpha_2)\)，因为函数是单峰的，所以极小值点必定位于点 \(\alpha_2\)的左侧，即 \(\alpha^*\in[a,\alpha_2]\)，搜索区间可以缩小为 \([a,\alpha_2]\)，如图 2-1(a) 所示；
2. \(f(\alpha_1)>f(\alpha_2)\)，极小值点必定位于点 \(\alpha_1\)的右侧，即 \(\alpha^*\in[\alpha_1,b]\)，搜索区间可以缩小为 \([\alpha_1,b]\)，如图 2-1(b) 所示；
3. \(f(\alpha_1)=f(\alpha_2)\)，极小值点必定位于点 \(\alpha_1\)和 \(\alpha_2\)之间，即 \(\alpha^*\in[\alpha_1,\alpha_2]\)，搜索区间可缩小为 \([\alpha_1,\alpha_2]\)，如图 2-1(c) 所示。

图 2-1 搜索区间缩小示意图

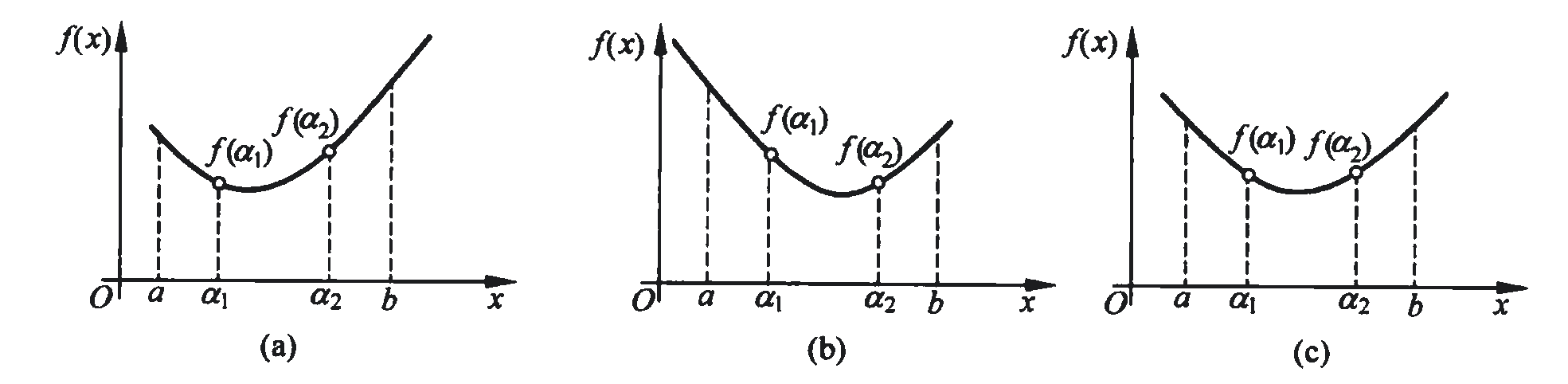
根据上述方法，可在新搜索区间里再取两个新点比较函数值来继续缩小区间，但这样做效率较低，应该考虑利用已经计算过的区间内剩下的那个点。对于以上的 (1)、(2) 两种情况，可以在新搜索区间内取一点 \(x_3\)和该区间内剩下的那个点（第 (1) 种情况的 \(\alpha_1\)点或第 (2) 种情况的 \(\alpha_2\)点）进行函数值的比较来继续缩短搜索区间。而第 (3) 种情况则要取两个新点进行比较，为统一起见，将前面 3 种情况综合为以下两种情况:

1. 若 \(f(\alpha_1)< f(\alpha_2)\)，则将搜索区间缩小为 \([a,\alpha_2]\)
2. 若 \(f(\alpha_2)\ge f(\alpha_2)\)，则将搜索区间缩小为 \([\alpha_1,b]\)。

2.2 黄金分割法原理

黄金分割法就是基于上述原理来选择区间内计算点的位置的，它有以下要求：

1. 点 \(\alpha_1\)和 \(\alpha_2\)相对区间 \([a,b]\)的边界要对称布置，即区间 \([a,\alpha_1)\)的大小与区间 \((\alpha_2,b]\)的大小相等；
2. 每次计算一个新点，要求保留的区间长度 \(l\)与原区间长度 \(L\)之比等于被消去的区间长度 \(L-l\)与保留区间长度 \(l\)之比，即要求下式成立：

   \[\frac lL=\frac{L-l}l\tag{2-1}\]

令

\[\lambda=\frac lL\]

将上式代入式 \(\fml{2-1}\)，有

\[\lambda^2+\lambda-1=0\tag{2-2}\]

求解式 \(\fml{2-2}\)，得

\[\lambda=\frac{\sqrt5-1}2\approx0.618\]

该方法保证每次迭代都以同一比率缩小区间，缩短率为 \(0.618\)，故黄金分割法又称为 \(0.618\)法。保留的区间长度为整个区间长度的 \(0.618\)倍，消去的区间长度为整个区间长度的 \(0.382\)倍。

黄金分割法的计算步骤如下：

图 2-2 黄金分割法原理

1. 在 \([a,b]\)内取两点 \(\alpha_1\)， \(\alpha_2\)，如图 2-2(a) 所示，使

   \[\begin{align}\alpha_1&=a+0.382(b-a)\\\alpha_2&=a+0.618(b-a)\end{align}\]

   令 \(f_1=f(\alpha_1)\)， \(f_2=f(\alpha_2)\)。
2. 比较 \(f_1\)和 \(f_2\)。当 \(f_1< f_2\)时，消去区间 \((\alpha_2,b]\)。做置换 \(b=\alpha_2\)， \(\alpha_2=\alpha_1\)并另取新点 \(\alpha_1=a+0.382(b-a)\)，如图 2-2(b) 所示，令 \(f_1=f(\alpha_1)\)。当 \(f_1\ge f_2\)时，消去区间 \([a,\alpha_1)\)。做置换 \(a=\alpha_1\)， \(\alpha_1=\alpha_2\)， \(f_1=f_2\)，并另取新点 \(\alpha_2=a+0.618(b-a)\)，如图 2-2(c) 所示，令 \(f_2=f(\alpha_2)\)。
3. 检查终止条件。若 \(b-a\le\epsilon\)，则输出最优解 \(\alpha^*=\frac12(a+b)\)和最优值 \(f(\alpha^*)\)；否则转第 (2) 步。

3. 如何使用

RMVL 中提供了一维寻优的函数 rm::fminbnd ，以下展示了一维寻优的例子。

3.1 创建项目

1. 添加源文件 main.cpp

   #include <cstdio>
   #include <rmvl/core/numcal.hpp>
    
   // 自定义函数 f(x)=x²+4x-3
   inline double quadratic(double x) { return x * x + 4 * x - 3; }
    
   int main()
   {
       // 确定搜索区间
       auto [x1, x2] = rm::region(quadratic, 0);
       // 添加优化选项（容许误差和最大迭代次数）
       rm::OptimalOptions options;
       options.max_iter = 100; // 最大迭代次数是 100，不加以设置默认是 1000
       options.tol = 1e-4;     // 容许误差是 1e-4，不加以设置默认是 1e-6
       // 一维寻优
       auto [x, fval] = rm::fminbnd(quadratic, x1, x2, options);
       printf("x    = %f\n", x);
       printf("fval = %f\n", fval);
   }

2. 添加 CMakeLists.txt

   cmake_minimum_required(VERSION 3.10)
   project(FminbndDemo)
   find_package(RMVL COMPONENTS core REQUIRED)
   add_executable(demo main.cpp)
   target_link_libraries(demo PRIVATE rmvl_core)

3.2 构建、运行

在项目根目录打开终端，输入

mkdir build
cd build
cmake ..
cmake --build . --parallel 4
./demo

可以看到运行结果

x    = -2.000000
fval = -7.000000