 |
RMVL
1.5.0-dev
Robotic Manipulation and Vision Library
|
 |
RMVL
1.5.0-dev
Robotic Manipulation and Vision Library
|
卡尔曼滤波详细公式推导
上一篇教程:基于 TOPSIS 模型的熵权法 ↑
下一篇教程:扩展卡尔曼滤波 ↓
相关类 rm::KalmanFilter
\[ \def\red#1{\color{red}{#1}} \def\teal#1{\color{teal}{#1}} \def\green#1{\color{green}{#1}} \def\transparent#1{\color{transparent}{#1}} \def\orange#1{\color{orange}{#1}} \def\Var{\mathrm{Var}} \def\Cov{\mathrm{Cov}} \def\tr{\mathrm{tr}} \def\fml#1{\text{(#1)}} \]
卡尔曼滤波器是一个 Optimal Recursive Data Processing Algorithm,即最优化递归数字处理算法,与其说滤波器,倒不如说这是一个 观测器 。简单来说,卡尔曼滤波器能够估计目标的当前位置,并结合观测结果,以最高置信度获得当前位置。
示例
我们需要测量一个硬币的长度 \(x\),现测出了如下结果
\[\begin{align}z_1&=30.2\mathrm{mm}\\z_2&=29.7\mathrm{mm}\\z_3&=30.1\mathrm{mm}\\&\vdots\end{align}\]
我们要利用这些观测结果来估计硬币的真实长度,很自然的我们可以想到使用取平均的方式,我们可以利用 \(k\) 个观测值,求出硬币长度在第 \(k\) 次的估计值 \(\hat x_k\)。
\[\hat x_k=\frac{z_1+z_2+\cdots+z_k}k\tag{1-1}\]
这是一条非常简单的取算数平均的公式,但是我们为了估计硬币的长度,需要用到所有的观测值,例如我们已经测了 5 次硬币的长度,并且使用公式 \(\fml{1-1}\) 得到了第 5 次的平均值(长度的估计值),在测完第 6 次长度准备计算第 6 次估计值的时候,使用公式 \(\fml{1-1}\) 还需要重新使用前 5 次的观测值。当观测次数非常高的时候,计算的压力就逐渐高起来了。
针对这一问题,我们可以改写公式 \(\fml{1-1}\)
\[\begin{align}\hat x_k&=\frac1k(z_1+z_2+\cdots+z_k)\\ &=\frac1k(z_1+z_2+\cdots+z_{k-1})+\frac1kz_k\\ &=\frac{k-1}k·\frac1{\red{k-1}}\red{(z_1+z_2+\cdots+z_{k-1})}+\frac1kz_k\\ &=\frac{k-1}k\red{\hat x_{k-1}}-\frac1kz_k\\&=\hat x_{k-1}-\frac1k\hat x_{k-1}+\frac1kz_k\\ &=\hat x_{k-1}+\frac1k(z_k-\hat x_{k-1})\tag{1-2a}\end{align}\]
这样我们就把硬币长度的估计值,改写成由上一次估计值和当前观测值共同作用的形式。并且我们发现,随着测量次数 \(k\) 增大, \(\frac1k\) 趋向于 \(0\), \(\hat x_k\) 趋向于 \(\hat x_{k-1}\),这也就是说,随着 \(k\) 增长,测量结果将不再重要。
为了不失一般性,我们把公式 \(\fml{1-2a}\) 的结果改写成以下形式。
\[\boxed{\hat x_k=\hat x_{k-1}+\red{K_k}(z_k-\hat x_{k-1})}\tag{1-2b}\]
其中 \(K_k\) 表示 Kalman Gain,即卡尔曼增益。对于 \(K_k\),我们先给出他的计算结果。
\[K_k=\frac{e_{{EST}_{k-1}}}{e_{{EST}_{k-1}}+e_{{MEA}_k}}\tag{1-3}\]
其中, \(e_{{EST}_{k-1}}\) 表示第 \(k-1\) 次的估计误差, \(e_{{MEA}_k}\) 表示第 \(k\) 次的测量误差。可以得到,在 \(k\) 时刻,
现在我们可以使用公式 \(\fml{1-2b}\) 的思想来研究数据融合。如果有一辆车以恒定速度行驶,现在得到了两个数据:
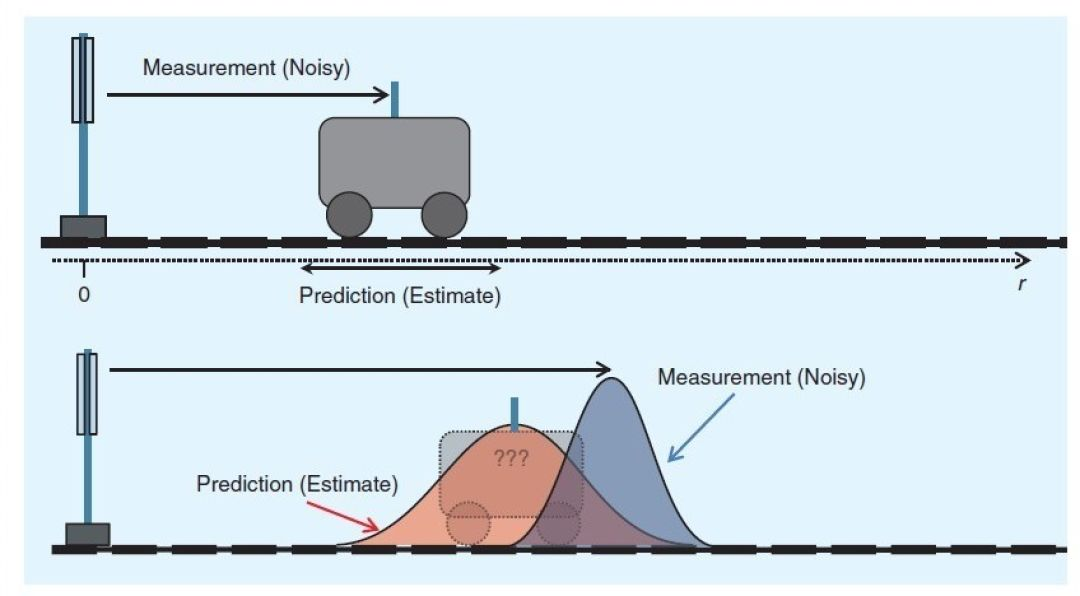
由于自身的原因,它的位置并不是由匀速运动公式得到的精确位置,它的距离传感器数据也不完全准确。两者都有一定的误差。那么我们现在如何估计汽车的实际位置呢?
我们使用公式 \(\fml{1-2b}\) 的思想,得到估计值
\[\hat x=\teal{x_1}+\green{K_k}(\red{x_2}-\teal{x_1})\tag{1-4}\]
我们的目标很明确,希望求出这个 \(\green{K_k}\),使得估计值 \(\hat x\) 是最优的,即 \(\hat x\) 的方差 \(\Var(\hat x)\) 最小,即 \(\hat x\to x_{实际值}\)。
不妨令 \(\left\{\begin{align}\teal{x_1=30\mathrm m\qquad\sigma_1=2\mathrm m}\\\red{x_2=32\mathrm m\qquad\sigma_2=4\mathrm m}\end{align}\right.\),则有
\[\begin{align}\Var(\hat x)&=\Var[x_1+K_k(x_2-x_1)]\\&=\Var(x_1-K_kx_1+K_kx_2)\\ &=\Var[(1-K_k)x_1+K_kx_2]\\由x_1和x_2相互独立\quad&=\Var[(1-k)x_1]+\Var(K_kx_2)\\ &=(1-K_k)^2\Var(x_1)+K_k^2\Var(x_2)\\ &=(1-K_k)^2\sigma_1^2+K_k^2\sigma_2^2\tag{1-5}\end{align}\]
要求 \(\Var(\hat x)\) 的最小值,只需令 \(\mathrm \Var(\hat x)'|_{K_k}=0\) 即可,即:
\[\frac{\mathrm d\Var(\hat x)}{\mathrm dK_k}=-2(1-K_k)\sigma_1^2+2K_k\sigma_2^2=0\tag{1-6}\]
即
\[K_k=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2}\tag{1-7}\]
代入数据后,有
\[\left\{\begin{align} K_k&=\frac{2^2}{2^2+4^2}=0.2\\ \hat x&=30+0.2(32-30)=30.4\mathrm m\quad\orange{理论最优解}\\ \sigma_{\hat x}^2&=(1-0.2)^22^2+0.2^24^2=3.2\quad(\sigma_{\hat x}=1.79) \end{align}\right.\]
| 数据 | \(x\) | \(y\) | \(z\) |
|---|---|---|---|
| \(1\) | \(x_1\) | \(y_1\) | \(z_1\) |
| \(2\) | \(x_2\) | \(y_2\) | \(z_2\) |
| \(3\) | \(x_3\) | \(y_3\) | \(z_3\) |
| 平均值 | \(\bar x\) | \(\bar y\) | \(\bar z\) |
方差
表明单个变量的波动程度
\[\begin{align} \Var(x)&=\frac13\left[(x_1-\bar x)^2+(x_2-\bar x)^2+(x_3-\bar x)^2\right]=\frac13\sum_{i=1}^3(x-\bar x)^2\stackrel{\triangle}{=}\sigma_x^2\\ \Var(y)&=\frac13\left[(y_1-\bar y)^2+(y_2-\bar y)^2+(y_3-\bar y)^2\right]=\frac13\sum_{i=1}^3(y-\bar y)^2\stackrel{\triangle}{=}\sigma_y^2\\ \Var(z)&=\frac13\left[(z_1-\bar z)^2+(z_2-\bar z)^2+(z_3-\bar z)^2\right]=\frac13\sum_{i=1}^3(z-\bar z)^2\stackrel{\triangle}{=}\sigma_z^2 \end{align}\]
一般的,方差具有以下推导公式
\[\begin{align}\Var(X)&=\frac1n\sum_{i=1}^n(X-\bar X)^2\\&=\frac1n\sum_{i=1}^n(X-EX)^2\\ 定义\quad&=\green{E\left[(X-EX)^2\right]}\\ &=E\left[X^2-2X·EX+(EX)^2\right]\\&=EX^2-2EX·EX+(EX)^2\\ &=\red{EX^2-(EX)^2}\tag{1-8}\end{align}\]
协方差
表明变量之间的相关性,为正数表示正相关,为负数表示负相关,绝对值越大表示相关性越强
\[\begin{align} \Cov(x,y)&=\frac13\left[(x_1-\bar x)(y_1-\bar y)+(x_2-\bar x)(y_2-\bar y)+(x_3-\bar x)(y_3-\bar y)\right]\\ &=\frac13\sum_{i=1}^3(x-\bar x)(y-\bar y)\stackrel{\triangle}{=}\sigma_x\sigma_y\\ \Cov(y,z)&=\frac13\left[(y_1-\bar y)(z_1-\bar z)+(y_2-\bar y)(z_2-\bar z)+(y_3-\bar y)(z_3-\bar z)\right]\\ &=\frac13\sum_{i=1}^3(y-\bar y)(z-\bar z)\stackrel{\triangle}{=}\sigma_y\sigma_z\\ \Cov(x,z)&=\frac13\left[(x_1-\bar x)(z_1-\bar z)+(x_2-\bar x)(z_2-\bar z)+(x_3-\bar x)(z_3-\bar z)\right]\\ &=\frac13\sum_{i=1}^3(x-\bar x)(z-\bar z)\stackrel{\triangle}{=}\sigma_x\sigma_z \end{align}\]
一般的,协方差具有以下推导公式
\[\begin{align}\Cov(X,Y) &=\frac1n\sum_{i=1}^n(X-\bar X)(Y-\bar Y)\\ &=\frac1n\sum_{i=1}^n(X-EX)(Y-EY)\\ 定义\quad&=\green{E\left[(X-EX)(Y-EY)\right]}\\ &=E(XY-X·EY-Y·EX+EX·EY)\\ &=E(XY)-EX·EY-EY·EX+EX·EY\\ &=\red{E(XY)-EXEY} \tag{1-9}\end{align}\]
协方差矩阵
按照协方差的定义出发,可以有
\[\begin{align}\Cov(x_i,x_j) &=E\left[(x_i-Ex_i)(x_j-Ex_j)\right]=\sigma_{x_i}\sigma_{x_j}\\ 令误差e_i=x_i-E(x_i)\quad&=\green{E(e_ie_j)} \tag{1-10a}\end{align}\]
若取 \(i,j=1,2,\cdots,n\),则可以得到协方差矩阵 \(P\),表示为
\[\begin{align}P&=\begin{bmatrix} \sigma_{x_1}^2&\sigma_{x_1}\sigma_{x_2}&\cdots&\sigma_{x_1}\sigma_{x_n}\\ \sigma_{x_2}\sigma_{x_1}&\sigma_{x_2}^2&\cdots&\sigma_{x_2}\sigma_{x_n}\\ \vdots&\vdots&\ddots&\vdots\\ \sigma_{x_n}\sigma_{x_1}&\sigma_{x_n}\sigma_{x_2}&\cdots&\sigma_{x_n}^2 \end{bmatrix}\\&=\begin{bmatrix}Ee_1^2&Ee_1Ee_2&\cdots&Ee_1Ee_n\\ Ee_2Ee_1&Ee_2^2&\cdots&Ee_2Ee_n\\\vdots&\vdots&\ddots&\vdots\\ Ee_nEe_1&Ee_nEe_2&\cdots&Ee_n^2\end{bmatrix}\\&= E\begin{bmatrix}e_1^2&e_1e_2&\cdots&e_1e_n\\ e_2e_1&e_2^2&\cdots&e_2e_n\\\vdots&\vdots&\ddots&\vdots\\ e_ne_1&e_ne_2&\cdots&e_n^2\end{bmatrix}=\green{E\left(\pmb e\pmb e^T\right)}\tag{1-10b}\end{align}\]
对于一个系统,可以使用状态空间方程来描述其运动
\[\left\{\begin{align} \dot{\pmb x}&=F\pmb x+G\pmb u\\ \pmb z&=H\pmb x \end{align}\right.\tag{1-11}\]
根据 3.4 方程组的 Runge-Kutta 公式 中精确解的公式 \(\text{(b)}\),我们可以知道状态空间方程的解的表达式,即
\[\pmb x(t)=e^{F(t-t_0)}\pmb x(t_0)+\int_{t_0}^te^{F(t-\tau)}G\pmb u(\tau)\mathrm d\tau\tag{1-12}\]
以 \(T\)为周期离散采样+零阶保持器,可以得到
\[\begin{align} \pmb x(t_k)&=e^{F(t_k-t_{k-1})}\pmb x(t_{k-1})+\int_{t_{k-1}}^{t_k}e^{F(t_k-\tau)}G\pmb u(\tau)\mathrm d\tau\\ &=e^{FT}\pmb x(t_{k-1})+\int_{t_{k-1}}^{t_k}e^{F(t_k-\tau)}\mathrm d\tau·G\pmb u(t_{k-1})\\ &=e^{FT}\pmb x(t_{k-1})+\left[-F^{-1}e^{F(t_k-\tau)}\right]_{t_{k-1}}^{t_k}·G\pmb u(t_{k-1})\\ &=e^{FT}\pmb x(t_{k-1})+F^{-1}(e^{FT}-I)G\pmb u(t_{k-1})\\ \pmb x_k&=\red{e^{FT}}\pmb x_{k-1}+\green{F^{-1}(e^{FT}-I)G}\pmb u_{k-1}\\ 简记为\quad\pmb x_k&=\red A\pmb x_{k-1}+\green B\pmb u_{k-1}\tag{1-13a}\end{align}\]
因此我们可以得到离散系统的状态空间方程
\[\left\{\begin{align} \pmb x_k&=A\pmb x_{k-1}+B\pmb u_{k-1}\\ \pmb z_k&=H\pmb x_k \end{align}\right.\tag{1-13b}\]
这其实是个不准确的结果,因为如果我们考虑上噪声,公式 \(\fml{1-13b}\) 应该改写为
\[\left\{\begin{align} \pmb x_k&=A\pmb x_{k-1}+B\pmb u_{k-1}\red{+\pmb w_{k-1}}&p(\pmb w)\sim N(0,Q)\\ \pmb z_k&=H\pmb x_k\red{+\pmb v_k}&p(\pmb v)\sim N(0,R) \end{align}\right.\tag{1-13c}\]
\[Q=E(\pmb w\pmb w^T)=\begin{bmatrix}\sigma_{w_1}^2&\sigma_{w_1}\sigma_{w_2}&\cdots&\sigma_{w_1}\sigma_{w_n}\\ \sigma_{w_2}\sigma_{w_1}&\sigma_{w_2}^2&\cdots&\sigma_{w_2}\sigma_{w_n}\\ \vdots&\vdots&\ddots&\vdots\\\sigma_{w_n}\sigma_{w_1}&\sigma_{w_n}\sigma_{w_2}&\cdots&\sigma_{w_n}^2\end{bmatrix}\]
称为过程噪声协方差矩阵\[R=E(\pmb v\pmb v^T)=\begin{bmatrix}\sigma_{v_1}^2&\sigma_{v_1}\sigma_{v_2}&\cdots&\sigma_{v_1}\sigma_{v_n}\\ \sigma_{v_2}\sigma_{v_1}&\sigma_{v_2}^2&\cdots&\sigma_{v_2}\sigma_{v_n}\\ \vdots&\vdots&\ddots&\vdots\\\sigma_{v_n}\sigma_{v_1}&\sigma_{v_n}\sigma_{v_2}&\cdots&\sigma_{v_n}^2\end{bmatrix}\]
称为测量噪声协方差矩阵但是,这两个误差我们无从得知,我们只能使用公式 \(\fml{1-13b}\) 的形式进行近似估计,通过 \(\pmb x_k=A\pmb x_{k-1}+B\pmb u_{k-1}\) 算出来的 \(\pmb x_k\) 称为先验状态估计,一般写为
\[\red{\hat{\pmb x}_k^-=A\pmb x_{k-1}+B\pmb u_{k-1}\tag{1-14}}\]
通过 \(\pmb z_k=H\pmb x_k\) 得到的 \(\pmb x_k\) 是测出来的结果,记为 \(\hat{\pmb x}_{k_{MEA}}\),即
\[\hat{\pmb x}_{k_{MEA}}=H^+\pmb z_k\tag{1-15}\]
因为 \(H^{-1}\) 可能不存在,这里先使用 M-P 广义逆 \(H^+\) 来表示。
\[A\pmb x=\pmb b\]
必定存在最小二乘解\[\pmb x=(A^TA)^{-1}A^T\pmb b\]
可以令 \(A^+=(A^TA)^{-1}A^T\) 来表示 Moore-Penrose 广义逆,即\[\pmb x=A^+\pmb b\]
当 \(A\) 可逆时, \(A^+=A^{-1}\).目前的两个结果 \(\hat{\pmb x}_k^-\) 和 \(\hat{\pmb x}_{k_{MEA}}\) 都不准确,因此可以回顾 1.3 数据融合 的部分,在公式 \(\fml{1-4}\) 中使用了算出来的 \(\teal{x_1}\) 和测出来的 \(\red{x_2}\) 得到了最优估计值 \(\hat x\),为此我们可以仿照这一步骤来求出离散系统状态的最优估计值 \(\hat{\pmb x}_k\),称为后验状态估计。
\[\begin{align}\hat{\pmb x}_k&=\hat{\pmb x}_k^-+\green{G_k}(\hat{\pmb x}_{k_{MEA}}-\hat{\pmb x}_k^-)\\ &=\hat{\pmb x}_k^-+\green{G_k}(H^+\pmb z_k-\hat{\pmb x}_k^-)\tag{1-16}\end{align}\]
令 \(G_k=K_kH\),可以得到
\[\red{\hat{\pmb x}_k=\hat{\pmb x}_k^-+K_k(\pmb z_k-H\hat{\pmb x}_k^-)\tag{1-17}}\]
我们的目标依然很明确,希望求出这个 \(\green{K_k}\),使得后验状态估计值 \(\hat{\pmb x}_k\) 是最优的,即 \(\hat{\pmb x}_k\) 的方差 \(\Var(\hat{\pmb x}_k)\) 最小,即 \(\hat{\pmb x}_k\to \pmb x_k\)。如何衡量 \(\hat{\pmb x}_k\) 的方差 \(\Var(\hat{\pmb x}_k)\)?我们可以令状态误差 \(\pmb e_k=\pmb x_k-\hat{\pmb x}_k\),那么此时 \(p(\pmb e_k)\sim N(0,P_k)\),其中 \(P_k\) 是误差协方差矩阵,并且满足
\[P_k=\begin{bmatrix}\sigma_{e_1}^2&\cdots&\sigma_{e_1}\sigma_{e_n}\\\vdots&&\vdots\\\sigma_{e_n}\sigma_{e_1}&\cdots&\sigma_{e_n}^2\end{bmatrix}\tag{1-18}\]
方差 \(\Var(\hat{\pmb x}_k)\) 最小,即 \(\sum\limits_{i=1}^{n}\sigma_{e_i}^2\) 最小,即 \(P_k\) 的迹 \(\tr(P_k)\) 最小。
对于状态误差,有
\[\begin{align} \pmb e_k&=\pmb x_k-\hat{\pmb x}_k=\pmb x_k-\left(\hat{\pmb x}_k^-+K_k(\pmb z_k-H\hat{\pmb x}_k^-)\right)\\ &=\pmb x_k-\hat{\pmb x}_k^--K_k\pmb z_k+K_kH\hat{\pmb x}_k^-\\ &=\pmb x_k-\hat{\pmb x}_k^--K_k(H\pmb x_k+\pmb v_k)+K_kH\hat{\pmb x}_k^-\\ &=\pmb x_k-\hat{\pmb x}_k^--K_kH\pmb x_k-K_k\pmb v_k+K_kH\hat{\pmb x}_k^-\\ &=(\pmb x_k-\hat{\pmb x}_k^-)-K_kH(\pmb x_k-\hat{\pmb x}_k^-)-K_k\pmb v_k\\ &=(I-K_kH)\teal{(\pmb x_k-\hat{\pmb x}_k^-)}-K_k\pmb v_k\\ &=(I-K_kH)\teal{\pmb e_k^-}-K_k\pmb v_k\tag{1-19}\end{align}\]
则误差协方差矩阵可以表示为
\[\begin{align}P_k &=E\left(\pmb e_k\pmb e_k^T\right)=E\left[(\pmb x_k-\hat{\pmb x}_k)(\pmb x_k-\hat{\pmb x}_k)^T\right]\\ &=E\left[\left((I-K_kH)\teal{\pmb e_k^-}-K_k\pmb v_k\right)\left((I-K_kH)\teal{\pmb e_k^-}-K_k\pmb v_k\right)^T\right]\\ &=E\left[\left(\green{(I-K_kH)\pmb e_k^-}-\red{K_k\pmb v_k}\right)\left(\teal{{\pmb e_k^-}^T(I-K_kH)^T}-\orange{\pmb v_k^TK_k^T}\right)\right]\\ &=E\left[\green{(I-K_kH)\pmb e_k^-}\teal{{\pmb e_k^-}^T(I-K_kH)^T}-\green{(I-K_kH)\pmb e_k^-}\orange{\pmb v_k^TK_k^T}-\right.\\ &\transparent=\left.\red{K_k\pmb v_k}\teal{{\pmb e_k^-}^T(I-K_kH)^T}+\red{K_k\pmb v_k}\orange{\pmb v_k^TK_k^T}\right]\\ &=\red{E(}(I-K_kH)\pmb e_k^-{\pmb e_k^-}^T(I-K_kH)^T\red{)}-\\ &\transparent=\red{E(}(I-K_kH)\pmb e_k^-\pmb v_k^TK_k^T\red{)}-\\ &\transparent=\red{E(}K_k\pmb v_k{\pmb e_k^-}^T(I-K_kH)^T\red{)}+\\ &\transparent=\red{E(}K_k\pmb v_k\pmb v_k^TK_k^T\red{)}\\ 提出常数的期望\quad&=(I-K_kH)\red{E(}\pmb e_k^-{\pmb e_k^-}^T\red{)}(I-K_kH)^T-\\ &\transparent=(I-K_kH)\red{E(}\pmb e_k^-\pmb v_k^T\red{)}K_k^T-\\ &\transparent=K_k\red{E(}\pmb v_k{\pmb e_k^-}^T\red{)}(I-K_kH)^T+\\ &\transparent=K_k\red{E(}\pmb v_k\pmb v_k^T\red{)}K_k^T\\ &=(I-K_kH)\red{P_k^-}(I-K_kH)^T+\\ \pmb e_k^-和{\pmb v_k}^T相互独立\quad&\transparent=0+\\ 且期望为0\quad&\transparent=0+\\ &\transparent=K_k\red{R}K_k^T\\ &=\left(\green{P_k^-}-\red{K_kHP_k^-}\right)\left(\teal I-\orange{H^TK_k^T}\right)+K_kRK_k^T\\ &=\green{P_k^-}-\red{K_kHP_k^-}-\green{P_k^-}\orange{H^TK_k^T}+\red{K_kHP_k^-}\orange{H^TK_k^T}+K_kRK_k^T\\ P_k^-对称\quad&=P_k^--K_kHP_k^--\left(K_kHP_k^-\right)^T+K_kHP_k^-H^TK_k^T+K_kRK_k^T \tag{1-20}\end{align}\]
因此, \(P_k\) 的迹可以表示为
\[\tr(P_k)=\tr(P_k^-)-2\tr(K_kHP_k^-)+\tr(K_kHP_k^-H^TK_k^T)+\tr(K_kRK_k^T)\tag{1-21}\]
希望 \(\tr(P_k)\) 有最小值,则需要对 \(K_k\) 求导,则有
\[\frac{\mathrm d\tr(P_k)}{\mathrm dK_k}=0-2\frac{\mathrm d\tr(K_kHP_k^-)}{\mathrm dK_k}+\frac{\mathrm d\tr(K_kHP_k^-H^TK_k^T)}{\mathrm dK_k}+\frac{\mathrm d\tr(K_kRK_k^T)}{\mathrm dK_k}=0\tag{1-22}\]
对于形如 \(\frac{\mathrm d\tr(AB)}{A}\) 的导数计算,可以通过拿一个 2 阶矩阵作为例子
令
\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix},\quad B=\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}\]
则
\[AB=\begin{bmatrix}a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{21}+a_{12}b_{22}\\a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\end{bmatrix}\]
则
\[\tr(AB)=a_{11}b_{11}+a_{12}b_{21}+a_{21}b_{12}+a_{22}b_{22}\]
则
\[\frac{\mathrm d\tr(AB)}{\mathrm dA}=\begin{bmatrix}\frac{\partial\tr(AB)}{\partial a_{11}}&\frac{\partial\tr(AB)}{\partial a_{12}}\\\frac{\partial\tr(AB)}{\partial a_{21}}&\frac{\partial\tr(AB)}{\partial a_{22}}\end{bmatrix}=\begin{bmatrix}b_{11}&b_{21}\\b_{12}&b_{22}\end{bmatrix}=B^T\]
因此可以得到
\[\frac{\mathrm d\tr(AB)}{A}=B^T\tag{1-23a}\]
同理,我们也能验证如下结论
\[\begin{align}\frac{\mathrm d\tr(ABA^T)}{A}&=AB+AB^T\\ 当B对称时\quad&=2AB\end{align}\tag{1-23b}\]
那么,公式 \(\fml{1-22}\)可以写为
\[\begin{align}2\frac{\mathrm d\tr(K_kHP_k^-)}{\mathrm dK_k} &=\frac{\mathrm d\tr(K_kHP_k^-H^TK_k^T)}{\mathrm dK_k}+\frac{\mathrm d\tr(K_kRK_k^T)}{\mathrm dK_k}\\ 2{P_k^-}^TH^T&=2K_kHP_k^-H^T+2K_kR\\ P_k^-H^T&=K_k\left(HP_k^-H^T+R\right) \tag{1-24}\end{align}\]
最终可以得到误差协方差矩阵的迹最小时的卡尔曼增益 \(K_k\) 的表达式
\[\red{K_k=P_k^-H^T\left(HP_k^-H^T+R\right)^{-1}\tag{1-25}}\]
讨论
我们在计算卡尔曼增益 \(K_k\) 的时候出现了 \(E\left(\pmb e_k^-{\pmb e_k^-}^T\right)\),并使用 \(P_k^-\) 进行表示,代表先验的误差协方差矩阵,现在要做的就是求出先验误差协方差矩阵 \(P_k^-\),同样可以由协方差矩阵的定义出发。
首先先求 \(\pmb e_k^-\)
\[\begin{align}\pmb e_k^-&=\pmb x_k-\hat{\pmb x}_k^-\\ &=A\pmb x_{k-1}+B\pmb u_{k-1}+\pmb w_{k-1}-A\hat{\pmb x}_{k-1}-B\pmb u_{k-1}\\ &=A(\pmb x_{k-1}-\hat{\pmb x}_{k-1})+\pmb w_{k-1}\\ &=A\pmb e_{k-1}+\pmb w_{k-1}\tag{1-26}\end{align}\]
因此先验误差协方差矩阵 \(P_k^-\) 可以表示为
\[\begin{align}P_k^- &=E\left(\pmb e_k^-{\pmb e_k^-}^T\right)=E\left[(A\pmb e_{k-1}+\pmb w_{k-1})(A\pmb e_{k-1}+\pmb w_{k-1})^T\right]\\ &=E\left[(A\pmb e_{k-1}+\pmb w_{k-1})(\pmb e_{k-1}^TA^T+\pmb w_{k-1}^T)\right]\\ &=E\left[A\pmb e_{k-1}\pmb e_{k-1}^TA^T+A\pmb e_{k-1}\pmb w_{k-1}^T+\pmb w_{k-1}\pmb e_{k-1}^TA^T+\pmb w_{k-1}\pmb w_{k-1}^T\right]\\ &=AE(\pmb e_{k-1}\pmb e_{k-1}^T)A^T+AE\pmb e_{k-1}E\pmb w_{k-1}^T+E\pmb w_{k-1}E\pmb e_{k-1}^TA^T+E(\pmb w_{k-1}\pmb w_{k-1}^T)\\ &=AP_{k-1}A^T+0+0+Q \tag{1-27}\end{align}\]
最终可以得到先验误差协方差矩阵的表达式
\[\red{P_k^-=AP_{k-1}A^T+Q\tag{1-28}}\]
在求解 \(P_k^-\) 的时候用到了 \(P_{k-1}\),因此需要进一步求解 \(P_k\),从而为下一次 \(P_{k+1}^-\) 所使用。
由 1.5 卡尔曼增益推导 的公式 \(\fml{1-20}\) 可以得到
\[\begin{align}P_k &=\green{P_k^-}-\red{K_kHP_k^-}-\green{P_k^-}\orange{H^TK_k^T}+\red{K_kHP_k^-}\orange{H^TK_k^T}+K_kRK_k^T\\ &=P_k^--K_kHP_k^--P_k^-H^TK_k^T+K_k(HP_k^-H^T+R)K_k^T\\ 代入\fml{1-25}\quad&=P_k^--K_kHP_k^--P_k^-H^TK_k^T+P_k^-H^TK_k^T\\ &=P_k^--K_kHP_k^-\tag{1-29}\end{align}\]
即所谓后验误差协方差矩阵 \(P_k\)
\[\red{P_k=(I-K_kH)P_k^-\tag{1-30}}\]
至此,Kalman Filter 的 5 大公式已经全部求出,分别是公式 \(\fml{1-14}\)、公式 \(\fml{1-17}\)、公式 \(\fml{1-25}\)、公式 \(\fml{1-28}\) 和公式 \(\fml{1-30}\)
按照处理顺序,卡尔曼滤波器划分为两个部分
① 预测
\[\hat{\pmb x}_k^-=A\pmb x_{k-1}+B\pmb u_{k-1}\]
\[P_k^-=AP_{k-1}A^T+Q\]
② 校正(更新)
\[K_k=P_k^-H^T\left(HP_k^-H^T+R\right)^{-1}\]
\[\hat{\pmb x}_k=\hat{\pmb x}_k^-+K_k(\pmb z_k-H\hat{\pmb x}_k^-)\]
\[P_k=(I-K_kH)P_k^-\]
首先必须要寻找 RMVL 包,即 find_package(RMVL REQUIRED),之后可直接在 CMakeLists.txt 中链接库
这里的 xxx 为需要链接到 core 模块的目标
取
Tp = doubleStateDim = 4MeatureDim = 2可以得到以下代码
 1.12.0
1.12.0