 |
RMVL
2.5.0-dev
Robotic Manipulation and Vision Library
|
 |
RMVL
2.5.0-dev
Robotic Manipulation and Vision Library
|
从 向量到子空间距离 和 构建法方程 两种方式推导了最小二乘法的矩阵表示
最小二乘法诞生于统计学,其最初的目标是使用一条直线拟合一系列离散的点,那么我们该如何寻找这一直线?最小二乘法的原理是使得拟合直线的误差的平方和最小。这里的误差定义成每一个离散的点 \(x_i\)与拟合直线的 距离 。在这一最初的用法中,点到直线的距离能够很直观的描述成点到直线的 垂线 的长度。
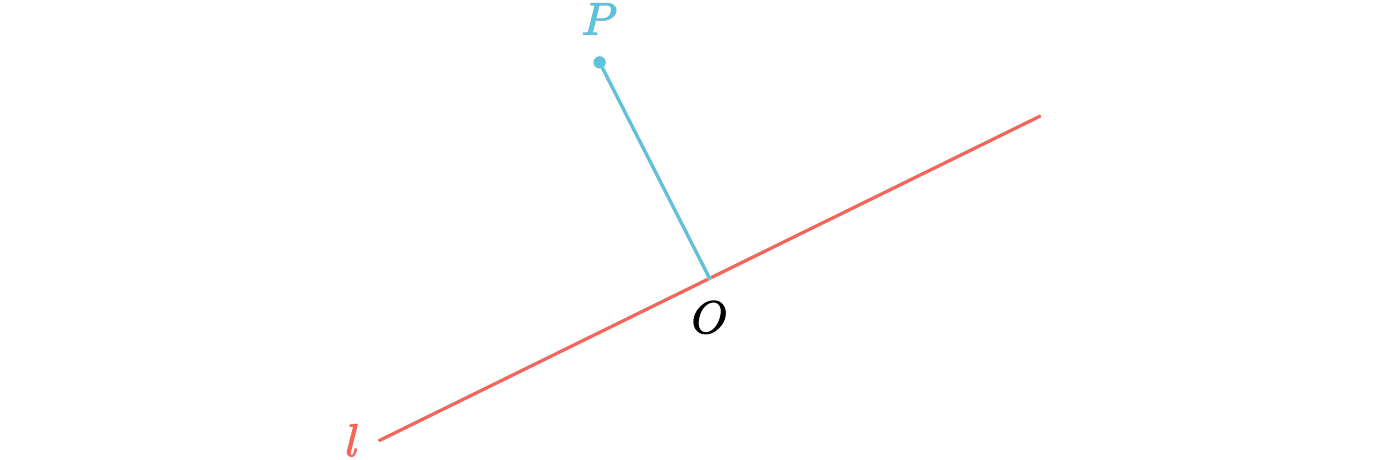
如图 1-1 所示,令直线外一点为 \(P\),直线为 \(l\),垂线为 \(l_0\),垂足为点 \(O\)。最小二乘法就是构建一条直线,使得这些点 \(P_i\)到这条直线的距离平方和最小,此时 \(O_i\)点被称为 最小二乘解 。
让我们拓宽最小二乘这一概念。对于一个向量 \(\boldsymbol\alpha\)所表示的直线,在该直线上是否存在一点 \(Y\)使得 \(Y\)到直线外一点 \(P\)的距离最小?答案是肯定的,并且原理与图 1 完全一致,即构造 \(P\)到直线的垂线,在线性代数中我们引入过 内积 运算,并且得知两个向量 正交 (垂直)的时候,二者内积为 \(0\)。
在初等几何中,点到直线(或平面)上所有点的距离以垂线最短。同样的,对于一个 欧式空间 \(V=\mathbb{R}^n\),一个指定向量 \(\boldsymbol\beta\in V\) 和子空间 \(W\subseteq V\) 的各个向量距离也以 垂线 最短。换句话说,该向量 \(\boldsymbol\beta\) 与子空间 \(W\) 正交,记作 \(\boldsymbol\beta\perp W\)。其中子空间可以表示成
\[W=L(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_s)\tag{1-1}\]
其中 \(\boldsymbol\alpha_1,\ \boldsymbol\alpha_2,\ \cdots,\ \boldsymbol\alpha_s\) 是一 \(W\) 的一组基。从上式可以推导出,若 \(\exists\boldsymbol\beta\in V\),使得 \(\boldsymbol\beta\perp W\),则对于 \(\forall\boldsymbol\alpha\in W\),均有 \(\boldsymbol\beta\perp\boldsymbol\alpha\)。因此可以写为
\[\begin{matrix} (\boldsymbol\alpha_1,\boldsymbol\beta)&=&\boldsymbol\alpha_1^T\boldsymbol\beta&=&0\\ (\boldsymbol\alpha_2,\boldsymbol\beta)&=&\boldsymbol\alpha_2^T\boldsymbol\beta&=&0\\ \vdots&=&\vdots&=&\vdots\\ (\boldsymbol\alpha_s,\boldsymbol\beta)&=&\boldsymbol\alpha_s^T\boldsymbol\beta&=&0 \end{matrix}\tag{1-2a}\]
观察中间一列 \(\boldsymbol\alpha_i^T\boldsymbol\beta\),可以写成
\[(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_i)^T\boldsymbol\beta=\boldsymbol 0\tag{1-2b} \]
我们先用一个最简单的例子。
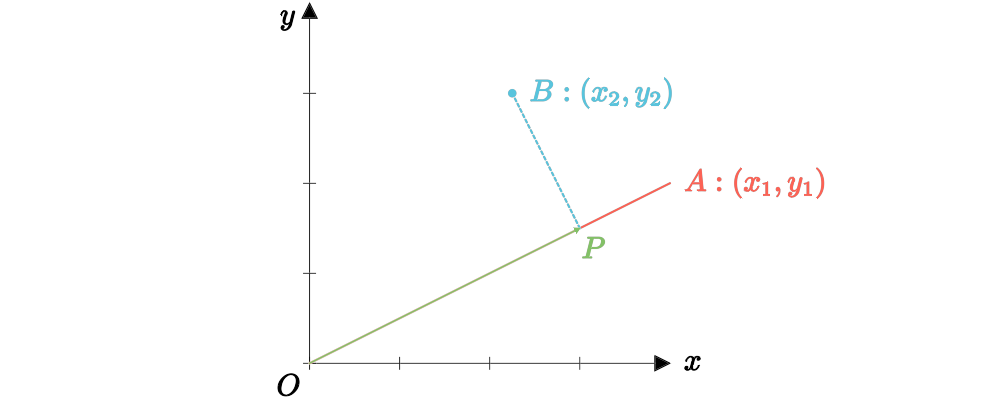
对于图 1-2 中使用向量表示的方式,最小二乘解可以表示为向量 \(OP\)的坐标,在这种情况下, \(BP\)与 \(OA\)垂直,即:
\[\left(OA,BP\right)=0\tag{1-3}\]
我们令 \(OA=\boldsymbol a\), \(OB=\boldsymbol b\),待求向量 \(OP=\boldsymbol y\),( \(\boldsymbol a, \boldsymbol b, \boldsymbol y\) 均为列向量)代入公式 \(\text{(1-3)}\) 可以得到
\[(\boldsymbol a,\ \boldsymbol y-\boldsymbol b)=0\tag{1-4}\]
其中 \(\boldsymbol y-\boldsymbol b\) 就是公式 \(\text{(1-2a)}\) 中的 \(\boldsymbol\beta\),写成矩阵形式
\[\boldsymbol a^T(\boldsymbol y-\boldsymbol b)=0\tag{1-5}\]
为此我们得到了最小二乘解 \(\boldsymbol y\) 的表达式,这也为后文超定线性方程组的最小二乘解提供了理论基础。
有时候我们会遇到这一类形如 \(A\boldsymbol x=\boldsymbol b\) 的方程组
\[\left\{\begin{align}2x_1+x_2&=1\\x_1-x_2&=0\\x_1+x_2&=2\end{align}\right.\qquad\Leftrightarrow\qquad \begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}1\\0\\2\end{bmatrix}\tag{2-1}\]
这里 \(A=\begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\), \(\boldsymbol b=(1,0,2)^T\),在图 1-3 中表示如下。
一般的,对于一个系数矩阵 \(A=(a_{ij})_{s\times{n}}\), \(\boldsymbol b=(b_1,b_2,\cdots,b_s)^T\), \(\boldsymbol x=(x_1,x_2,\cdots,x_s)^T\),若满足 \(\text{rank}(A)\leq s\) 时,线性方程组没有数值解,但我们希望找到一组 最优解 ,衡量此最优解的方法仍然可以采用最小二乘法。设法找出一组解 \(\hat{\boldsymbol x}=(x_1^0,\ x_2^0,\ x_3^0,\ \cdots,\ x_n^0)\) 使得每一项的误差 \(\delta_i\) 平方和最小,如何定量这个误差?能否继续采用上文最小二乘法的点到直线的最短距离的思想作为出发点?答案是肯定的,这里先给出误差平方和的表达式。
\[\delta^2=\sum_{i=0}^{s-1}(a_{i1}x_1+a_{i2}x_2+\cdots+a_{in}x_n-b_i)^2\tag{2-2}\]
上式也可以写成
\[\delta^2=\sum_{i=0}^{s-1}\left[\left(\sum_{j=1}^na_{ij}x_j\right)-b_i\right]^2\tag{2-3a}\]
或
\[\delta^2=\left\|\left(\sum_{j=1}^na_{ij}x_j\right)-b_i\right\|_2^2\tag{2-3b}\]
上式的基本想法是,将线性方程组的每一个方程在带入 \(\hat{\boldsymbol x}\) 后与右端项 \(b_i\) 作差,即可得到每一项的误差 \(\delta_i\),我们令 \(\boldsymbol y=A\boldsymbol x\),则 \(\boldsymbol y\) 当然是个 \(s\) 维列向量,上述平方偏差 \(\delta^2\) 也就是 \(|\boldsymbol y-\boldsymbol b|^2\),而最小二乘法就是要找一组 \(\hat{\boldsymbol x}\) 使得 \(|\boldsymbol y-\boldsymbol b|^2\) 最小,换句话说,就是要使 \(\boldsymbol y\) 与 \(\boldsymbol b\) 的距离最小。
到这里,我们需要进一步强化线性方程组及其生成空间的这些概念。
基本概念介绍
\[T(V)=\{T\boldsymbol\alpha|\boldsymbol\alpha\in V\}\]
是 \(V\) 的子空间,因此方程组的系数矩阵 \(A\) 就可以当做是某个线性变换 \(T(V)\) 对应的矩阵,表示为\[(T\boldsymbol\alpha_1,T\boldsymbol\alpha_2,\cdots,T\boldsymbol\alpha_n)=(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_n)A\]
\(T(V)\) 的维数叫线性变换 \(T\) 的秩,也可以记为 \(\text{rank}(A)\)。因此列空间也可以被称为象子空间;\[K=\{\boldsymbol\alpha\in V|T\boldsymbol\alpha=\boldsymbol0\}\]
是 \(V\) 的子空间,称为线性变换 \(T\) 的核,记作 \(T^{-1}(\boldsymbol0)\),因此解空间也被称为核空间。另外,在方程组中,解空间的极大线性无关组被称为 基础解系 ,即解空间的任意一个向量都可由基础解系所线性表出,即 \(\boldsymbol x=k_1\boldsymbol\xi_1+k_2\boldsymbol\xi_2+\cdots+k_t\boldsymbol\xi_t\),不难得出结论, \(T^{-1}(\boldsymbol0)\) 的维度就是 \(t\)。并且可以证明出如下的 子空间维数定理 :设 \(T\) 是 \(n\) 维线性空间 \(V\) 的线性变换,则一定满足维数关系\[\text{dim}T(V)+\text{dim}T^{-1}(\boldsymbol0)=n\]
也可以记为\[\text{rank}(A)+t=n\tag{2-4}\]
让我们继续回到最小二乘解的求解过程中,根据 \(\text{(1-2b)}\) 和 \(\text{(1-4)}\),类似的,我们可以构建出
\[\begin{matrix} (\boldsymbol\alpha_1,\boldsymbol y-\boldsymbol b)&=&\boldsymbol\alpha_1^T(\boldsymbol y-\boldsymbol b)&=&0\\ (\boldsymbol\alpha_2,\boldsymbol y-\boldsymbol b)&=&\boldsymbol\alpha_2^T(\boldsymbol y-\boldsymbol b)&=&0\\ \vdots&=&\vdots&=&\vdots\\ (\boldsymbol\alpha_n,\boldsymbol y-\boldsymbol b)&=&\boldsymbol\alpha_n^T(\boldsymbol y-\boldsymbol b)&=&0\\ \end{matrix}\tag{2-5}\]
这表示当 \(\boldsymbol y-\boldsymbol b\) 与列空间正交时, \(\boldsymbol y\) 与 \(\boldsymbol b\) 距离最短,与列空间正交就必须要与生成列空间的每一个向量即 \(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_n\) 正交。整合后可以得到
\[(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_n)^T(\boldsymbol y-\boldsymbol b)=\boldsymbol0\tag{2-6}\]
\(\boldsymbol\alpha_1,\boldsymbol\alpha_2,\cdots,\boldsymbol\alpha_n\) 刚好是系数矩阵按列分块的形式,又有 \(\boldsymbol y=A\hat{\boldsymbol x}\) 我们可以得到如下公式。
\[\begin{align} A^T(A\hat{\boldsymbol x}-\boldsymbol b)&=0\\ A^TA\hat{\boldsymbol x}&=A^T\boldsymbol b \end{align} \]
经过化简我们最终可以得到
\[\boxed{\hat{\boldsymbol x}=\left(A^TA\right)^{-1}A^T\boldsymbol b}\tag{2-7} \]
这就是最小二乘解所满足的代数方程。
下面给出 3 个示例,不直接使用公式 \(\text{(2-7)}\),通过几何或者其他手段来表示最小二乘解。
示例 1
问:求数 \(1,\ 2\) 的最小二乘解
显而易见,求算术平均数即可得到最小二乘解为 \(\frac32\)。但为何呢?
我们将其转化为一个线性方程组
\[\left\{\begin{align} x_1&=1\\ x_1&=2 \end{align}\right.\tag{3-1}\]
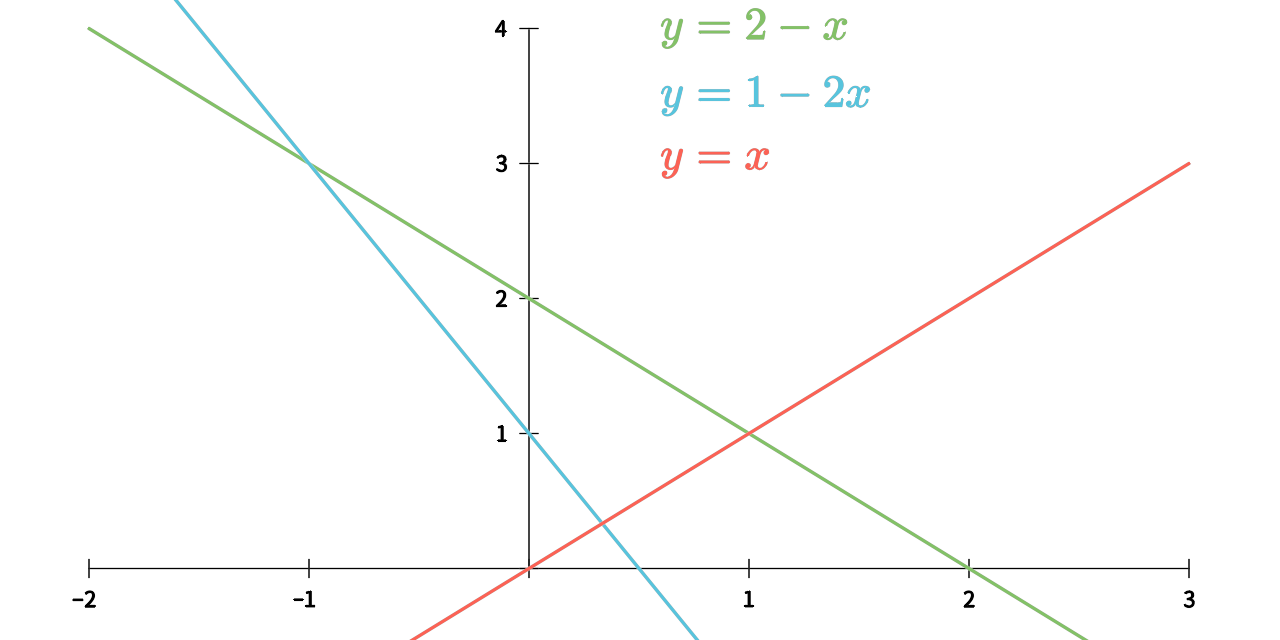
因此,系数矩阵 \(A=(1,\ 1)^T\),列空间 \(\boldsymbol y=A\boldsymbol x=(x_1,\ x_1)\),右端项为 \(\boldsymbol b=(1,\ 2)^T\)。可以画出一个平面笛卡尔坐标系,以表示这一列空间和指定向量 \(\boldsymbol b\),如图 2-1,满足
\[\left\{\begin{align} x&=x_1\\ y&=x_1 \end{align}\right.\tag{3-2}\]
这是一个参数方程,消去 \(x_1\) 可以得到 \(y=x\),这就是系数矩阵 \(A=(1,\ 1)^T\) 所生成的列空间。
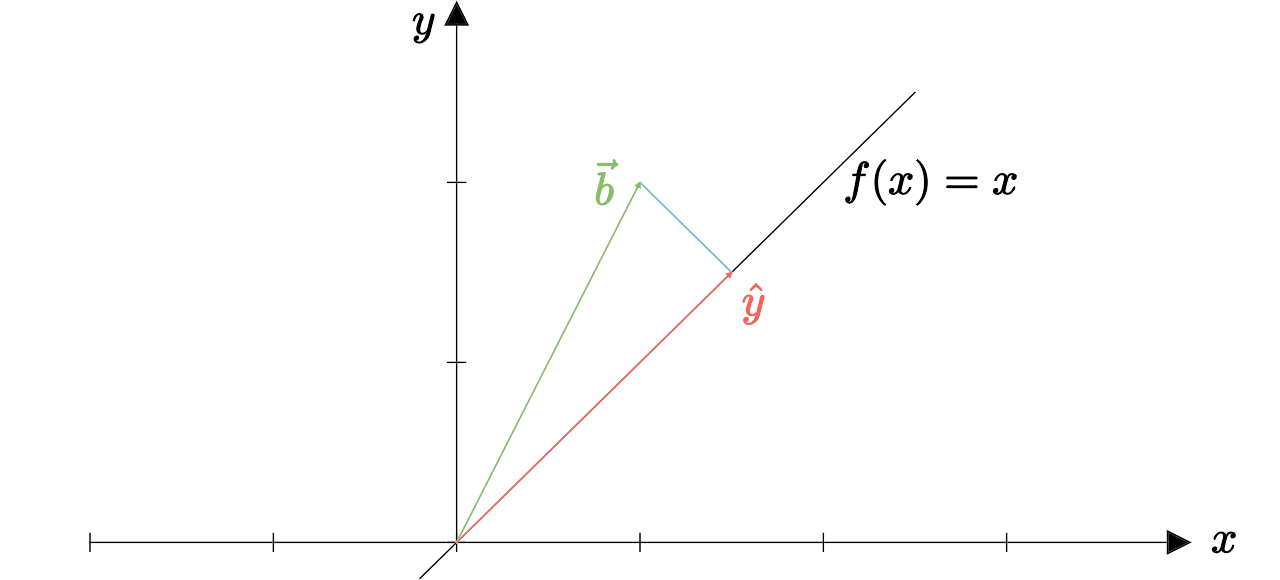
相当于现在需要在 \(y=x\) 上找到一个点,使得其到 \(\boldsymbol b\) 点的距离最短,这是初等几何的内容,做垂线即可,最终得到交点的坐标
\[\hat y=(\frac32,\frac32)\tag{3-3}\]
代入参数方程 \(\text{(3-2)}\),可以得到
\[x_1=\frac32\]
示例 2
题目:求公式 \(\text{(2-1)}\) 的最小二乘解
系数矩阵: \(A=\begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\),其生成的列空间为图 2-2 中橙色的平面,记作平面 \(\alpha\),并对 \(A\) 作列分块得到 \(A=(\boldsymbol\alpha_1,\boldsymbol\alpha_2)\)
列空间外向量(右端项): \(\boldsymbol b=(1,0,2)^T\)
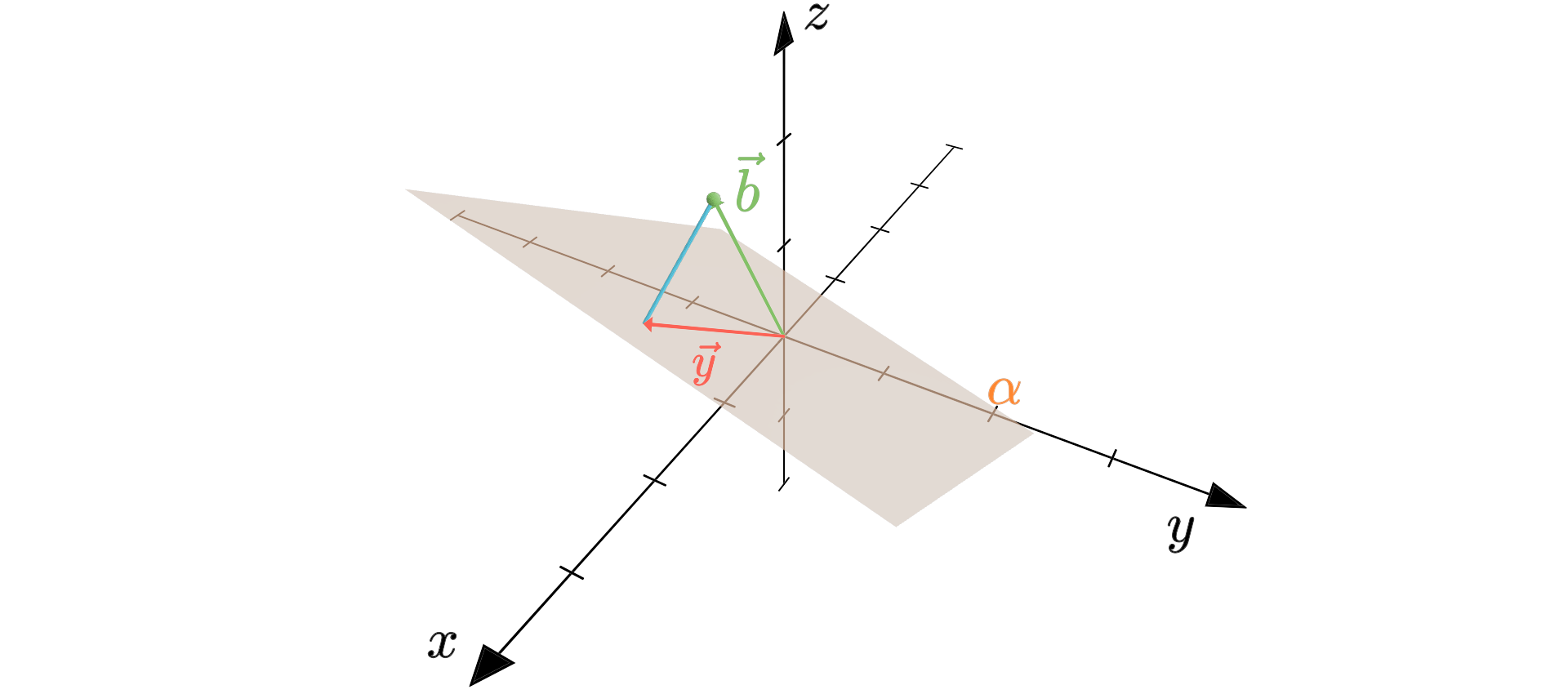
需要满足 \((\boldsymbol y-\boldsymbol b)\perp\alpha\),则需要分别满足 \((\boldsymbol y-\boldsymbol b)\perp\boldsymbol\alpha_1\) 和 \((\boldsymbol y-\boldsymbol b)\perp\boldsymbol\alpha_2\),下面使用几何法对最小二乘法的原理进行验证。
① 求平面 \(\alpha\) 的法向量 \(\boldsymbol n\)
\[\boldsymbol n=\left|\begin{matrix}\boldsymbol i&\boldsymbol j&\boldsymbol k\\1&-1&1\\2&1&1\end{matrix}\right| =-2\boldsymbol i+\boldsymbol j+3\boldsymbol k=\begin{bmatrix}-2\\1\\3\end{bmatrix}\tag{3-4} \]
② 根据约束条件列方程
满足 2 个 约束条件 ,即
联立得到
\[k\boldsymbol n+\boldsymbol b=x_1\boldsymbol\alpha_1+x_2\boldsymbol\alpha_2\tag{3-5a}\]
即
\[\left\{\begin{align} -2k+1&=2x_1+x_2\\k&=x_1-x_2\\3k+2&=x_1+x_2 \end{align}\right.\tag{3-5b}\]
③ 求解 \(\hat{\boldsymbol x}\)
这是一个关于 \(k,x_1,x_2\) 的线性方程组,解得
\[X=(-\frac27,\frac37,\frac57)^T\tag{3-6}\]
因此我们得到了满足以上 约束条件 的解
\[\hat{\boldsymbol x}=\left(\frac37,\frac57\right)^T\tag{3-7}\]
示例 3
题目:使用形如 \(f(t)=a_0+a_1t\) 的曲线在已知点集上完成拟合(线性拟合)
\[\begin{array}{c|cccc}\text{下标}i&0&1&2&3\\\hline t_i&1&2&3&4\\f(t_i)&0&2&1&3\end{array}\]
上文研究的 线性空间 都是定义在数域 \(\mathbb P^n\) 上的欧式空间,实际上,对于系数属于 \(\mathbb P\),而未定元为 \(t\) 的所有次数小于 \(n\) 的多项式集合也构成一个 线性空间 ,记作
\[\mathbb P{[t]}_n=a_0+a_1t+a_2t^2+\cdots+a_{n-1}t^{n-1}=\sum_{i=0}^{n-1}a_it^i\tag{3-8}\]
可以很容易的找到一组基
\[\left\{\begin{matrix} \phi_0(t)&=&1\\\phi_1(t)&=&t\\\phi_2(t)&=&t^2\\\vdots&=&\vdots\\\phi_{n-1}(t)&=&t^{n-1}\\ \end{matrix}\right.\tag{3-9}\]
\[a_0+a_1t+a_2t^2+\cdots+a_{n-1}t^{n-1}=\sum_{i=0}^{n-1}a_it^i=0\]
只有零解 ,即 \(a_0=a_1=a_2=\cdots=a_{n-1}=0\),这是显然的。上面都是一些概念性的介绍,跟后文求解最小二乘解无关。回到示例 3的这一问题本身,我们可以根据表 3-1 的信息,得到
\[\left\{\begin{align} \phi_0(t_0)a_0+\phi_1(t_0)a_1&=f(t_0)\\ \phi_0(t_1)a_0+\phi_1(t_1)a_1&=f(t_1)\\ \phi_0(t_2)a_0+\phi_1(t_2)a_1&=f(t_2)\\ \phi_0(t_3)a_0+\phi_1(t_3)a_1&=f(t_3) \end{align}\right.\tag{3-10a}\]
即
\[\left\{\begin{align}a_0+a_1&=0\\a_0+2a_1&=2\\a_0+3a_1&=1\\a_0+4a_1&=3\end{align}\right.\tag{3-10b}\]
这就转化为了一个超定线性方程组 \(A\boldsymbol a=\boldsymbol f\),求解可直接使用公式 \(\text{(2-7)}\),一般的,其系数矩阵可以表示为
\[A=\begin{bmatrix} \phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\ \phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\ \vdots&\vdots&&\vdots\\ \phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1}) \end{bmatrix}\qquad\boldsymbol f=\begin{bmatrix} f(t_0)\\f(t_1)\\\vdots\\f(t_{s-1})\end{bmatrix}\tag{3-11}\]
后文将给出另外一种描述最小二乘法的做法,这种做法有别于上面构造向量与子空间垂直的方式,通过对误差平方和直接求其最小值来得到最小二乘解(两种方式结果均能推导出公式 \(\text{(2-7)}\),但出发点不同)。此外,要介绍的这个解法也同样适用于整个线性空间(包括欧式空间、多项式空间等线性空间)。
相关类 rm::CurveFitter
后文会以多项式空间为例,从 \(\delta^2\) 的极值(最小值)入手,通过对该误差平方和求导数的方式获得该最优解,这也是数值分析教材中普遍采用的做法。在本小节后,会使用这一方法求解示例 3的问题。
回顾公式 \(\text{(2-3b)}\): \(\sum\limits_{j=1}^na_{ij}x_j\) 的部分,这是对应于欧式空间 \(\mathbb R^n\) 的误差平方和的写法,这表示生成的位于列空间中的向量在基下的第 \(i\) 个分量(坐标)。对于多项式空间 \(\mathbb R{[t]}_n\),这部分的写法为 \(a_0+a_1t+\cdots+a_{n-1}t^{n-1}=\sum\limits_{j=0}^{n-1}a_jt^j\)。那么对于包含 \(s\) 个已知点的集合(每个点包含 \(t_i\) 和 \(f(t_i)\) 两部分),使用 \(\mathbb R{[t]}_n\) 即 \(\sum\limits_{j=0}^{n-1}a_jt^j=\sum\limits_{j=0}^{n-1}a_j\phi_j(t_i)\) 的多项式来拟合这些点集,其最小二乘解设为 \(f^*(t)\),此时的误差平方和的最小值可以表示成
\[\delta_\min^2=\sum_{i=0}^{s-1}\left[f(t_i)-f^*(t_i)\right]^2=\min\sum_{i=0}^{s-1}\left[f(t_i)-\sum\limits_{j=0}^{n-1}a_j\phi_j(t_i)\right]^2\tag{4-1}\]
要求解 \(a_0,a_1,\cdots,a_{n-1}\),这相当于求多元函数
\[F(a_0,a_1,\cdots,a_{n-1})=\sum_{i=0}^{s-1}\left[f(t_i)-\sum_{j=0}^{n-1}a_j\phi_j(t_i)\right]^2\tag{4-2}\]
的极小值点。按照求极值的必要条件,可以对上述多元函数求偏导,令其为 \(0\) 有
\[\frac{\partial F}{\partial a_k}=2\sum_{i=0}^{s-1}\left[f(t_i)-\sum_{j=0}^{n-1}a_j\phi_j(t_i)\right][-\phi_k(t_i)]=0\qquad(k=0,1,\cdots,n-1),\]
整理为
\[\sum_{j=0}^{n-1}\left[\sum_{i=0}^{s-1}\phi_k(t_i)\phi_j(t_i)\right]a_j=\sum_{i=0}^{s-1}\phi_k(t_i)f(t_i)\qquad(k=0,1,\cdots,n-1)\tag{4-3}\]
不同的 2 个数字向量的内积定义为 \((\boldsymbol\alpha,\boldsymbol\beta)=\sum\limits_{i=0}^sa_ib_i\),同样的,多项式不同的 2 个分量(例如 \(\phi_1(t)=t\) 和 \(\phi_2(t)=t^2\) 就是不同的分量)之间的内积可以定义为 \((\phi_p(t),\phi_q(t))=\sum\limits_{i=0}^{s-1}\phi_p(t_i)\phi_q(t_i)\),简记为 \((\phi_p,\phi_q)\)。则有
\[\left\{\begin{align} \sum_{i=0}^{s-1}\phi_k(t_i)\phi_j(t_i)&=(\phi_k,\phi_j)\\ \sum_{i=0}^{s-1}\phi_k(t_i)f(t_i)&=(\phi_k,f)\equiv d_k\\ \end{align}\right.\tag{4-4}\]
于是公式 \(\text{(4-3)}\) 可以写成
\[\sum_{j=0}^{n-1}(\phi_k,\phi_j)a_j=d_k\qquad(k=0,1,\cdots,n-1)\tag{4-5a}\]
或者展开写为
\[(\phi_k,\phi_0)a_0+(\phi_k,\phi_1)a_1+\cdots+(\phi_k,\phi_{n-1})a_{n-1}=d_k\qquad(k=0,1,\cdots,n-1)\tag{4-5b}\]
对每一个 \(k\) 值,可以一并写成如下形式
\[\left\{\begin{matrix} (\phi_0,\phi_0)a_0&+&(\phi_0,\phi_1)a_1&+&\cdots&+&(\phi_0,\phi_{n-1})a_{n-1}&=&d_0\\ (\phi_1,\phi_0)a_0&+&(\phi_1,\phi_1)a_1&+&\cdots&+&(\phi_1,\phi_{n-1})a_{n-1}&=&d_1\\ \vdots&&\vdots&&&&\vdots&=&\vdots\\ (\phi_{n-1},\phi_0)a_0&+&(\phi_{n-1},\phi_1)a_1&+&\cdots&+&(\phi_{n-1},\phi_{n-1})a_{n-1}&=&d_{n-1}\\ \end{matrix}\right.\tag{4-5c}\]
上式称为 \(a_0,a_1,\cdots,a_{n-1}\) 的法方程(组),是 \(n\) 阶线性方程组,其系数矩阵是
\[G=\begin{bmatrix} (\phi_0,\phi_0)&(\phi_0,\phi_1)&\cdots&(\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0)&(\phi_1,\phi_1)&\cdots&(\phi_1,\phi_{n-1})\\ \vdots&\vdots&&\vdots\\ (\phi_{n-1},\phi_0)&(\phi_{n-1},\phi_1)&\cdots&(\phi_{n-1},\phi_{n-1})\\ \end{bmatrix}\tag{4-6}\]
对于 \((\phi_p,\phi_q)\),依照公式 \(\text{(4-4)}\),可以写成矩阵的表示方式,即
\[\begin{align}(\phi_p,\phi_q)&=\sum_{i=0}^{s-1}\phi_p(t_i)\phi_q(t_i)\\&=[\phi_p(t_0),\phi_p(t_1),\cdots,\phi_p(t_{s-1})] \begin{bmatrix}\phi_q(t_0)\\\phi_q(t_1)\\\vdots\\\phi_q(t_{s-1})\end{bmatrix}\end{align}\tag{4-7}\]
因此对法方程系数矩阵 \(G\) 的第 \(k\ (k=0,1,\cdots,n-1)\) 行,有
\[[(\phi_k,\phi_0),(\phi_k,\phi_1),\cdots,(\phi_k,\phi_{n-1})]\\=[\phi_k(t_0),\phi_k(t_1),\cdots,\phi_k(t_{s-1})] \begin{bmatrix}\phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\\phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\\vdots&\vdots &&\vdots\\\phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1})\end{bmatrix}\tag{4-8}\]
将 \(k=0,1,\cdots,n-1\) 的行向量拼起来,得到
\[\begin{align}G&=\begin{bmatrix} (\phi_0,\phi_0)&(\phi_0,\phi_1)&\cdots&(\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0)&(\phi_1,\phi_1)&\cdots&(\phi_1,\phi_{n-1})\\ \vdots&\vdots&&\vdots\\ (\phi_{n-1},\phi_0)&(\phi_{n-1},\phi_1)&\cdots&(\phi_{n-1},\phi_{n-1})\\ \end{bmatrix}\\&=\begin{bmatrix} \phi_0(t_0)&\phi_0(t_1)&\cdots&\phi_0(t_{s-1})\\ \phi_1(t_0)&\phi_1(t_1)&\cdots&\phi_1(t_{s-1})\\ \vdots&\vdots&&\vdots\\ \phi_{n-1}(t_0)&\phi_{n-1}(t_1)&\cdots&\phi_{n-1}(t_{s-1})\\ \end{bmatrix}\begin{bmatrix} \phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\ \phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\ \vdots&\vdots&&\vdots\\ \phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1}) \end{bmatrix}\end{align}\tag{4-9}\]
将公式 \(\text{(3-11)}\) 中 \(A\) 的矩阵表示方式代入 \(\text{(4-9)}\) 可以得到 \(G=A^TA\),并且右端项 \(\boldsymbol d=A^T\boldsymbol f\),代入公式 \(\text{(4-5)}\) 可以得到
\[A^TA\boldsymbol a=A^T\boldsymbol f\tag{4-10}\]
即
\[\boxed{\hat{\boldsymbol a}=\left(A^TA\right)^{-1}A^T\boldsymbol f}\tag{4-11}\]
这与公式 \(\text{(2-7)}\) 完全一致。
此外,对于形如 \(G\boldsymbol a=\boldsymbol d\ (G=A^TA)\) 的方程组,我们在求解的时候可以使用平方根法,即 Cholesky 方法进行求解,OpenCV 中对应的枚举类型为 cv::DECOMP_CHOLESKY。
对于示例 3,可以依次计算出
\[\begin{align} (\phi_0,\phi_0)&=\sum_{i=0}^3\phi_0(t_i)\phi_0(t_i)=\sum_{i=0}^31\times1=4\\ (\phi_1,\phi_0)=(\phi_0,\phi_1)&=\sum_{i=0}^3\phi_0(t_i)\phi_1(t_i)=\sum_{i=0}^31\times t_i=1+2+3+4=10\\ (\phi_1,\phi_1)&=\sum_{i=0}^3\phi_1(t_i)\phi_1(t_i)=\sum_{i=0}^3t_i\times t_i=1+4+9+16=30\\ d_0=(\phi_0,f)&=\sum_{i=0}^3\phi_0(t_i)f(t_i)=\sum_{i=0}^31\times f(t_i)=0+2+1+3=6\\ d_1=(\phi_1,f)&=\sum_{i=0}^3\phi_1(t_i)f(t_i)=\sum_{i=0}^3t_i\times f(t_i)\\&=0+2\times2+3\times1+4\times3=19\\ \end{align}\tag{4-12}\]
得到
\[\begin{bmatrix}4&10\\10&30\end{bmatrix}\hat{\boldsymbol a}= \begin{bmatrix}6\\19\end{bmatrix}\tag{4-13}\]
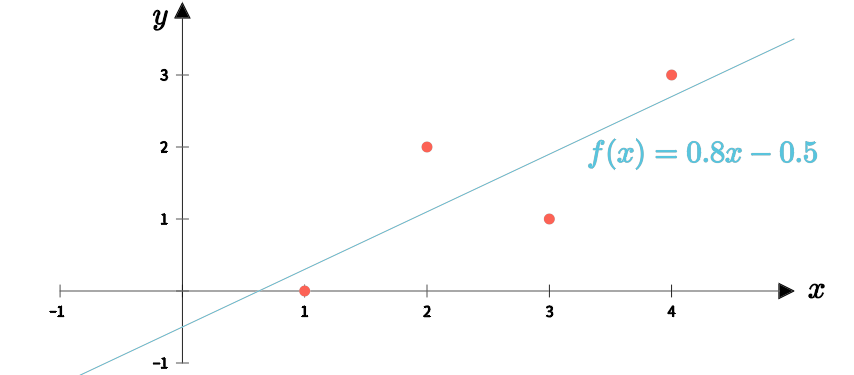
解得: \(\left\{\begin{align}a_0&=-0.5\\a_1&=0.8\end{align}\right.\),即拟合曲线为 \(y=-0.5+0.8t\),在图像中展示,如下。
OpenCV 中提供了最小二乘法求解的函数 cv::solve(),并设置有 2 个相关的成员函数,其函数原型如下。此外可参考 cv::solve 的 OpenCV 手册。
有关递推最小二乘法的介绍可参考 k 步前向预估能量机关预测 。