 |
RMVL
1.1.1
RoboMaster Vision Library
|
 |
RMVL
1.1.1
RoboMaster Vision Library
|
从一维进行 KalmanFilter 理论的介绍和公式推导,并在高维度进行类比和推广
相关类 rm::KalmanFilter
估计目标的当前位置,并以最高置信度获得当前位置。
如果有一辆车以恒定速度行驶,现在我得到两个数据:汽车的当前位置和汽车的当前距离传感器数据,根据匀速公式计算
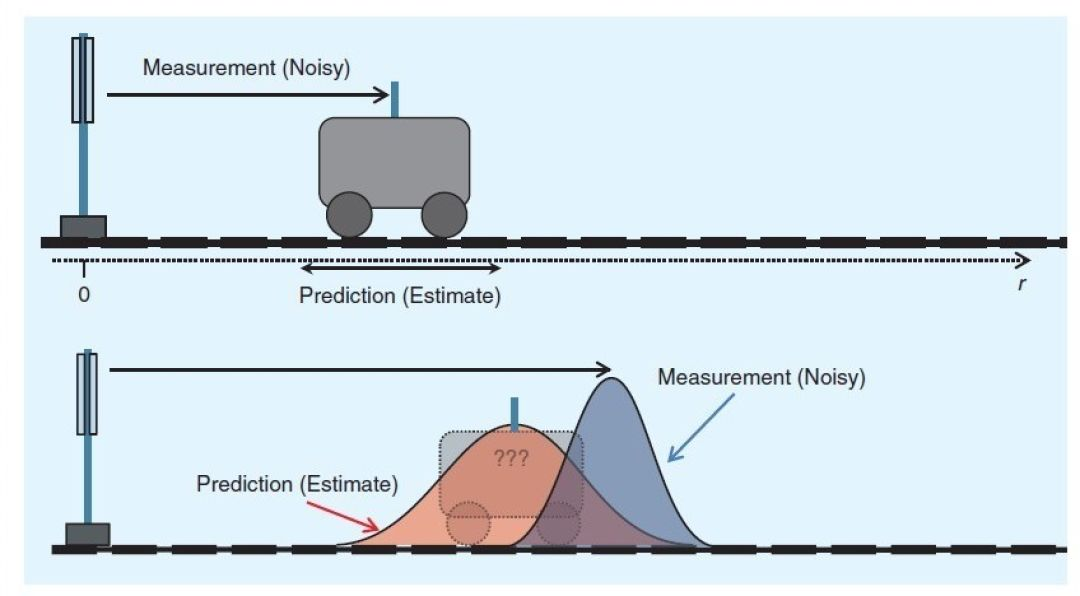
由于自身的原因,它的位置不是由匀速运动公式得到的精确位置,它的距离传感器数据也不完全准确。两者都有一定的误差。那么我们现在如何估计汽车的实际位置呢?
对于两者的置信度,不难想象,环境越复杂,公式得到的位置置信度越低。传感器越先进,置信度就越高。如果我们现在有了两条信息的置信度,我们就可以根据卡尔曼滤波对这两条数据进行处理,得到具有最高数学置信度的实际位置。
方差
\[ Var(x)=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n}\tag1 \]
协方差
\[ Cov(x,y)=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{n}\tag2 \]
如果使用同一个传感器多次测量一个数据(每次都会产生一个随机误差),就可以得到
\[ z_1,\ z_2,\ z_3\ \dots\ z_n \]
计算平均
\[ \begin{array}{lll} \hat x_n&=&\frac1n\sum\limits_{i=1}^nz_i\\ &=&\frac1n\sum\limits_{i=1}^{n-1}z_i+\frac1nz_n\\ &=&\frac{n-1}n\frac1{n-1}\sum\limits_{i=1}^{n-1}+\frac{1}{n}z_n\\ &=&\frac{n-1}{n}\hat{x}_{n-1}+\frac{1}{n}z_n\\ &=&\hat{x}_{n-1}+\frac{1}{n}(z_n-\hat{x}_{n-1})\\ &=&\hat{x}_{n-1}+K_n(z_n-\hat{x}_{n-1})\\ \end{array}\tag3 \]
\(K_n\): 卡尔曼增益
卡尔曼滤波的特点:只需要最后一帧的数据, 不需要 保留更多的数据。
若:
则:
\[ K_n=\frac{e_{EST_{n-1}}}{e_{EST_{n-1}}+e_{MEA_n}}\tag4 \]
\(e_{EST_{n-1}}\gg e_{MEA_n}\)
\[ K_n\rightarrow1\\ e\hat{x}_{n-1}=\hat{x}_{n-1}+z_n-\hat{x}_{n-1}=z_n\tag5 \]
\(e_{EST_{n-1}}\ll e_{MEA_n}\)
\[ K_n\rightarrow0\\ \hat{x}_n=\hat{x}_{n-1}\tag6 \]
Update:
\[ e_{EST_n}=(1-K_n)e_{EST_{n-1}}\tag7 \]
如果用两种不同的仪器同时测量一个数据(测量误差方差不同但已知),并且得到两个测量值: \(z_1,\ z_2\),我们如何选择最优估计值?
例如,如果 \(z_1,\ z_2\)的误差满足正态分布:
\[ z_1=30,\ S_1=2\\ z_2=32,\ S_2=4 \]
\[ \begin{array}{lll} \hat{z}&=&z_1+K(z_2-z_1)\qquad K\text{ is the parameter to be solved}\\ S_z^2&=&\text{Var}(z_1+K(z_2-z_1))\\ &=&\text{Var}((1-K)z_1+Kz_2)\\ &=&(1-K)^2\text{Var}(z_1)+K^2\text{Var}(z_2)\\ &=&(1-K)^2S_1^2+K^2S_2^2 \end{array}\tag8 \]
令
\[ \frac{\text{d}}{\text{d}x}((1-K)^2S_1^2+K^2S_2^2)=0\tag9 \]
求解公式 \((9)\),我们可以得到
\[ K=\frac{S_1^2}{S_1^2+S_2^2}\tag{10} \]
将 \(K\)代入下列公式
\[ \hat{z}=z_1+K(z_2-z_1) \]
则
\[ S_z^2=(1-K)^2S_1^2+K^2S_2^2\tag{11} \]
最终我们可以计算:
\[ K=0.2,\ z=30.4,\ S_z=1.79 \]
\[ \begin{array}{rrll} x_k&=&Ax_{k-1}+Bu_{k-1}+w_{k-1}&w\sim N(0,Q)\\ z_k&=&Hx_k+v_k&v\sim N(0, R) \end{array}\tag{12} \]
例如
\[ \begin{array}{rrl} p_k&=&p_{k-1}+v_{k-1}t+\frac12at^2\\v_k&=&v_{k-1}+at \end{array}\tag{13} \]
将公式 \((13)\)转换为矩阵表示
\[ \begin{bmatrix}p_k\\v_k\end{bmatrix} =\begin{bmatrix}1&t\\0&1\end{bmatrix} \begin{bmatrix}p_{k-1}\\v_{k-1}\end{bmatrix}+ \begin{bmatrix}\frac12t^2\\t\end{bmatrix} a+\begin{bmatrix}w_{p_k}\\w_{v_k}\end{bmatrix}\tag{14-1} \]
\[ \begin{bmatrix}z_{p_k}\\z_{v_k}\end{bmatrix}= \begin{bmatrix}1&0\\0&1\end{bmatrix} \begin{bmatrix}p_k\\v_k\end{bmatrix}+ \begin{bmatrix}v_{p_k}\\v_{v_k}\end{bmatrix}\tag{14-2} \]
\[ \begin{array}{rml} \hat x^-&=&A\hat x\\ P^-&=&APA^T+Q \end{array}\tag{15} \]
\[ \begin{array}{rml} K&=&P^-H^T(HP^-H^T+R)^{-1}\\ \hat x&=&\hat x^-+K(z-H\hat x^-)\\ P&=&(I-KH)P^-\end{array}\tag{16} \]
首先必须要寻找 RMVL 包,即 find_package(RMVL [OPTIONS]),之后可直接在中使用在 CMakeLists.txt 中链接库
取
Tp = doubleStateDim = 4MeatureDim = 4ControlDim = 1可以得到以下代码
 1.9.1
1.9.1