 |
RMVL
1.1.1
RoboMaster Vision Library
|
 |
RMVL
1.1.1
RoboMaster Vision Library
|
从 向量到子空间距离 ,和 构建法方程 两种方式推导了最小二乘法的矩阵表示
最小二乘法诞生于统计学,其最初的目标是使用一条直线拟合一系列离散的点,那么我们该如何寻找这一直线?最小二乘法的原理是使得拟合直线的误差的平方和最小。这里的误差定义成每一个离散的点 \(x_i\)与拟合直线的 距离 。在这一最初的用法中,点到直线的距离能够很直观的描述成点到直线的 垂线 的长度。
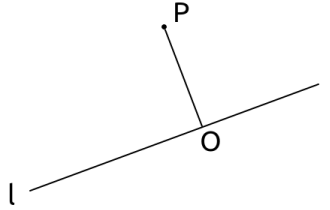
如图 1-1 所示,令直线外一点为 \(P\),直线为 \(l\),垂线为 \(l_0\),垂足为点 \(O\)。最小二乘法就是构建一条直线,使得这些点 \(P_i\)到这条直线的距离平方和最小,此时 \(O_i\)点被称为 最小二乘解 。
让我们拓宽最小二乘这一概念。对于一个向量 \(\pmb\alpha\)所表示的直线,在该直线上是否存在一点 \(Y\)使得 \(Y\)到直线外一点 \(P\)的距离最小?答案是肯定的,并且原理与图 1 完全一致,即构造 \(P\)到直线的垂线,在线性代数中我们引入过 内积 运算,并且得知两个向量 正交 (垂直)的时候,二者内积为 \(0\)。
在初等几何中,点到直线(或平面)上所有点的距离以垂线最短。同样的,对于一个 欧式空间 \(V=\mathbb{R}^n\),一个指定向量 \(\pmb\beta\in V\) 和子空间 \(W\subseteq V\) 的各个向量距离也以 垂线 最短。换句话说,该向量 \(\pmb\beta\) 与子空间 \(W\) 正交,记作 \(\pmb\beta\perp W\)。其中子空间可以表示成
\[W=L(\pmb\alpha_1,\pmb\alpha_2,\cdots,\pmb\alpha_s)\tag{1-1}\]
其中 \(\pmb\alpha_1,\ \pmb\alpha_2,\ \cdots,\ \pmb\alpha_s\) 是一 \(W\) 的一组基。从上式可以推导出,若 \(\exists\pmb\beta\in V\),使得 \(\pmb\beta\perp W\),则对于 \(\forall\pmb\alpha\in W\),均有 \(\pmb\beta\perp\pmb\alpha\)。因此可以写为
\[\begin{matrix} (\pmb\alpha_1,\pmb\beta)&=&\pmb\alpha_1^T\pmb\beta&=&0\\ (\pmb\alpha_2,\pmb\beta)&=&\pmb\alpha_2^T\pmb\beta&=&0\\ \vdots&=&\vdots&=&\vdots\\ (\pmb\alpha_s,\pmb\beta)&=&\pmb\alpha_s^T\pmb\beta&=&0 \end{matrix}\tag{1-2a}\]
观察中间一列 \(\pmb\alpha_i^T\pmb\beta\),可以写成
\[ (\pmb\alpha_1,\pmb\alpha_2,\cdots,\pmb\alpha_i)^T\pmb\beta=\pmb 0\tag{1-2b} \]
我们先用一个最简单的例子。
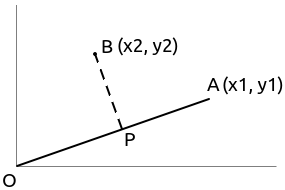
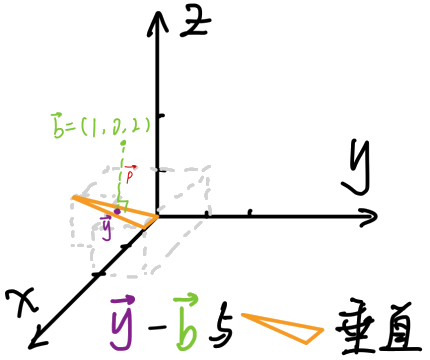
对于图 1-2 中使用向量表示的方式,最小二乘解可以表示为向量 \(OP\)的坐标,在这种情况下, \(BP\)与 \(OA\)垂直,即:
\[\left(OA,BP\right)=0\tag{1-3}\]
我们令 \(OA=\pmb a\), \(OB=\pmb b\),待求向量 \(OP=\pmb y\),( \(\pmb a, \pmb b, \pmb y\) 均为列向量)代入公式 \(\text{(1-3)}\) 可以得到
\[(\pmb a,\ \pmb y-\pmb b)=0\tag{1-4}\]
其中 \(\pmb y-\pmb b\) 就是公式 \(\text{(1-2a)}\) 中的 \(\pmb\beta\),写成矩阵形式
\[ \pmb a^T(\pmb y-\pmb b)=0\tag{1-5} \]
为此我们得到了最小二乘解 \(\pmb y\) 的表达式,这也为后文超定线性方程组的最小二乘解提供了理论基础。
有时候我们会遇到这一类形如 \(A\pmb x=\pmb b\) 的方程组
\[\left\{\begin{align}2x_1+x_2&=1\\x_1-x_2&=0\\x_1+x_2&=2\end{align}\right.\qquad\Leftrightarrow\qquad \begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}1\\0\\2\end{bmatrix}\tag{2-1}\]
这里 \(A=\begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\), \(\pmb b=(1,0,2)^T\),在图 1-3 中表示如下。
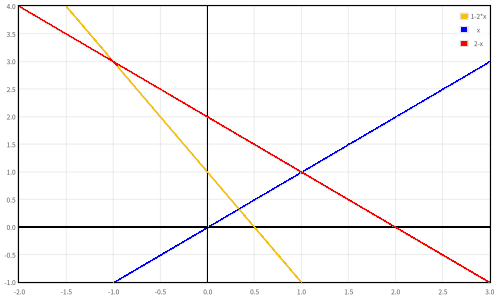
一般的,对于一个系数矩阵 \(A=(a_{ij})_{s\times{n}}\), \(\pmb b=(b_1,b_2,\cdots,b_s)^T\), \(\pmb x=(x_1,x_2,\cdots,x_s)^T\),若满足 \(\text{rank}(A)\leq s\) 时,线性方程组没有数值解,但我们希望找到一组 最优解 ,衡量此最优解的方法仍然可以采用最小二乘法。设法找出一组解 \(\hat{\pmb x}=(x_1^0,\ x_2^0,\ x_3^0,\ \cdots,\ x_n^0)\) 使得每一项的误差 \(\delta_i\) 平方和最小,如何定量这个误差?能否继续采用最小二乘法的点到直线的最短距离作为出发点?答案是肯定的,这里先给出误差平方和的表达式。
\[ \delta^2=\sum_{i=0}^{s-1}(a_{i1}x_1+a_{i2}x_2+\cdots+a_{in}x_n-b_i)^2\tag{2-2} \]
上式也可以写成
\[\delta^2=\sum_{i=0}^{s-1}\left[\left(\sum_{j=1}^na_{ij}x_j\right)-b_i\right]^2\tag{2-3a}\]
或
\[\delta^2=\left\|\left(\sum_{j=1}^na_{ij}x_j\right)-b_i\right\|_2^2\tag{2-3b}\]
上式的基本想法是,将线性方程组的每一个方程在带入 \(\hat{\pmb x}\) 后与右端项 \(b_i\) 作差,即可得到每一项的误差 \(\delta_i\),我们令 \(\pmb y=A\pmb x\),则 \(\pmb y\) 当然是个 \(s\) 维列向量,上述平方偏差 \(\delta^2\) 也就是 \(|\pmb y-\pmb b|^2\),而最小二乘法就是要找一组 \(\hat{\pmb x}\) 使得 \(|\pmb y-\pmb b|^2\) 最小,换句话说,就是要使 \(\pmb y\) 与 \(\pmb b\) 的距离最小。
到这里,我们需要进一步强化线性方程组及其生成空间的这些概念。
基本概念介绍
\[\text{rank}(A)+t=n\tag{2-4}\]
让我们继续回到最小二乘解的求解过程中,根据 \(\text{(1-2b)}\) 和 \(\text{(1-4)}\),类似的,我们可以构建出
\[\begin{matrix} (\pmb\alpha_1,\pmb y-\pmb b)&=&\pmb\alpha_1^T(\pmb y-\pmb b)&=&0\\ (\pmb\alpha_2,\pmb y-\pmb b)&=&\pmb\alpha_2^T(\pmb y-\pmb b)&=&0\\ \vdots&=&\vdots&=&\vdots\\ (\pmb\alpha_s,\pmb y-\pmb b)&=&\pmb\alpha_s^T(\pmb y-\pmb b)&=&0\\ \end{matrix}\tag{2-5}\]
这表示当 \(\pmb y-\pmb b\) 与列空间正交时, \(\pmb y\) 与 \(\pmb b\) 距离最短,与列空间正交就必须要与生成列空间的每一个向量即 \(\pmb\alpha_1,\pmb\alpha_2,\cdots,\pmb\alpha_s\) 正交。整合后可以得到
\[(\pmb\alpha_1,\pmb\alpha_2,\cdots,\pmb\alpha_s)^T(\pmb y-\pmb b)=\pmb0\tag{2-6}\]
\(\pmb\alpha_1,\pmb\alpha_2,\cdots,\pmb\alpha_s\) 刚好是系数矩阵按列分块的形式,又有 \(\pmb y=A\hat{\pmb x}\) 我们可以得到如下公式。
\[ \begin{align} A^T(A\hat{\pmb x}-\pmb b)&=0\\ A^TA\hat{\pmb x}&=A^T\pmb b \end{align} \]
经过化简我们最终可以得到
\[ \boxed{\hat{\pmb x}=\left(A^TA\right)^{-1}A^T\pmb b}\tag{2-7} \]
这就是最小二乘解所满足的代数方程。
下面给出 3 个示例,不直接使用公式 \(\text{(2-7)}\),通过几何或者其他手段来表示最小二乘解。
示例 1
问:求数 \(1,\ 2\) 的最小二乘解
显而易见,求算术平均数即可得到最小二乘解为 \(\frac32\)。但为何呢?
我们将其转化为一个线性方程组
\[\left\{\begin{align} x_1&=1\\ x_1&=2 \end{align}\right.\tag{3-1}\]
因此,系数矩阵 \(A=(1,\ 1)^T\),列空间 \(\pmb y=A\pmb x=(x_1,\ x_1)\),右端项为 \(\pmb b=(1,\ 2)^T\)。可以画出一个平面笛卡尔坐标系,以表示这一列空间和指定向量 \(\pmb b\),如图 2-1,满足
\[\left\{\begin{align} x&=x_1\\ y&=x_1 \end{align}\right.\tag{3-2}\]
这是一个参数方程,消去 \(x_1\) 可以得到 \(y=x\),这就是系数矩阵 \(A=(1,\ 1)^T\) 所生成的列空间。
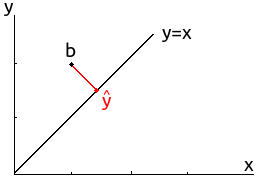
相当于现在需要在 \(y=x\) 上找到一个点,使得其到 \(\pmb b\) 的距离最短,这是初等几何的内容,做垂线即可,最终得到交点的坐标
\[(x,y)=(\frac32,\frac32)\tag{3-3}\]
代入参数方程 \(\text{(3-2)}\),可以得到
\[x_1=\frac32\]
示例 2
题目:求公式 \(\text{(2-1)}\) 的最小二乘解
系数矩阵: \(A=\begin{bmatrix}2&1\\1&-1\\1&1\end{bmatrix}\),其生成的列空间为图 2-2 中橙色的平面,记作平面 \(\alpha\),并对 \(A\) 作列分块得到 \(A=(\pmb\alpha_1,\pmb\alpha_2)\)
列空间外向量(右端项): \(\pmb b=(1,0,2)^T\)
需要满足 \((\pmb y-\pmb b)\perp\alpha\),则需要分别满足 \((\pmb y-\pmb b)\perp\pmb\alpha_1\) 和 \((\pmb y-\pmb b)\perp\pmb\alpha_2\),下面使用几何法对最小二乘法的原理进行验证。
① 求平面 \(\alpha\) 的法向量 \(\pmb n\)
\[ \pmb n=\left|\begin{matrix}\pmb i&\pmb j&\pmb k\\1&-1&1\\2&1&1\end{matrix}\right| =-2\pmb i+\pmb j+3\pmb k=\begin{bmatrix}-2\\1\\3\end{bmatrix}\tag{3-4} \]
② 根据约束条件列方程
满足 2 个 约束条件 ,即
联立得到
\[k\pmb n+\pmb b=x_1\pmb\alpha_1+x_2\pmb\alpha_2\tag{3-5a}\]
即
\[\left\{\begin{align} -2k+1&=2x_1+x_2\\k&=x_1-x_2\\3k+2&=x_1+x_2 \end{align}\right.\tag{3-5b}\]
③ 求解 \(\hat{\pmb x}\)
这是一个关于 \(k,x_1,x_2\) 的线性方程组,解得
\[X=(-\frac27,\frac37,\frac57)^T\tag{3-6}\]
因此我们得到了满足以上 约束条件 的解
\[\hat{\pmb x}=\left(\frac37,\frac57\right)^T\tag{3-7}\]
示例 3
题目:使用形如 \(f(t)=a_0+a_1t\) 的曲线在已知点集上完成拟合(线性拟合)
| 下标 \(i\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(t_i\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(f(t_i)\) | \(0\) | \(2\) | \(1\) | \(3\) |
上文研究的 线性空间 都是定义在数域 \(\mathbb P^n\) 上的欧式空间,实际上,对于系数属于 \(\mathbb P\),而未定元为 \(t\) 的所有次数小于 \(n\) 的多项式集合也构成一个 线性空间 ,记作
\[\mathbb P{[t]}_n=a_0+a_1t+a_2t^2+\cdots+a_{n-1}t^{n-1}=\sum_{i=0}^{n-1}a_it^i\tag{3-8}\]
可以很容易的找到一组基
\[\left\{\begin{matrix} \phi_0(t)&=&1\\\phi_1(t)&=&t\\\phi_2(t)&=&t^2\\\vdots&=&\vdots\\\phi_{n-1}(t)&=&t^{n-1}\\ \end{matrix}\right.\tag{3-9}\]
\[a_0+a_1t+a_2t^2+\cdots+a_{n-1}t^{n-1}=\sum_{i=0}^{n-1}a_it^i=0\]
只有零解 ,即 \(a_0=a_1=a_2=\cdots=a_{n-1}=0\),这是显然的。上面都是一些概念性的介绍,跟后文求解最小二乘解无关。回到示例 3的这一问题本身,我们可以根据表 3-1 的信息,得到
\[\left\{\begin{align} \phi_0(t_0)a_0+\phi_1(t_0)a_1&=f(t_0)\\ \phi_0(t_1)a_0+\phi_1(t_1)a_1&=f(t_1)\\ \phi_0(t_2)a_0+\phi_1(t_2)a_1&=f(t_2)\\ \phi_0(t_3)a_0+\phi_1(t_3)a_1&=f(t_3) \end{align}\right.\tag{3-10a}\]
即
\[\left\{\begin{align}a_0+a_1&=0\\a_0+2a_1&=2\\a_0+3a_1&=1\\a_0+4a_1&=3\end{align}\right.\tag{3-10b}\]
这就转化为了一个超定线性方程组 \(A\pmb a=\pmb f\),求解可直接使用公式 \(\text{(2-7)}\),一般的,其系数矩阵可以表示为
\[A=\begin{bmatrix} \phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\ \phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\ \vdots&\vdots&&\vdots\\ \phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1}) \end{bmatrix}\qquad\pmb f=\begin{bmatrix} f(t_0)\\f(t_1)\\\vdots\\f(t_{s-1})\end{bmatrix}\tag{3-11}\]
后文将给出另外一种描述最小二乘法的做法,这种做法有别于上面构造向量与子空间垂直的方式,通过对误差平方和直接求其最小值来得到最小二乘解(两种方式结果均能推导出公式 \(\text{(2-7)}\),但出发点不同)。此外,要介绍的这个解法也同样适用于整个线性空间(包括欧式空间、多项式空间等线性空间)。
后文会以多项式空间为例,从 \(\delta^2\) 的极值(最小值)入手,通过对该误差平方和求导数的方式获得该最优解,这也是数值分析教材中普遍采用的做法。在本小节后,会使用这一方法求解示例 3的问题。
回顾公式 \(\text{(2-3b)}\): \(\sum\limits_{j=1}^na_{ij}x_j\) 的部分,这是对应于欧式空间 \(\mathbb R^n\) 的误差平方和的写法,这表示生成的位于列空间中的向量在基下的第 \(i\) 个分量(坐标)。对于多项式空间 \(\mathbb R{[t]}_n\),这部分的写法为 \(a_0+a_1t+\cdots+a_{n-1}t^{n-1}=\sum\limits_{j=0}^{n-1}a_jt^j\)。那么对于包含 \(s\) 个已知点的集合(每个点包含 \(t_i\) 和 \(f(t_i)\) 两部分),使用 \(\mathbb R{[t]}_n\) 即 \(\sum\limits_{j=0}^{n-1}a_jt^j=\sum\limits_{j=0}^{n-1}a_j\phi_j(t_i)\) 的多项式来拟合这些点集,其最小二乘解设为 \(f^*(t)\),此时的误差平方和的最小值可以表示成
\[\delta_\min^2=\sum_{i=0}^{s-1}\left[f(t_i)-f^*(t_i)\right]^2=\min\sum_{i=0}^{s-1}\left[f(t_i)-\sum\limits_{j=0}^{n-1}a_j\phi_j(t_i)\right]^2\tag{4-1}\]
要求解 \(a_0,a_1,\cdots,a_{n-1}\),这相当于求多元函数
\[F(a_0,a_1,\cdots,a_{n-1})=\sum_{i=0}^{s-1}\left[f(t_i)-\sum_{j=0}^{n-1}a_j\phi_j(t_i)\right]^2\tag{4-2}\]
的极小值点。按照求极值的必要条件,可以对上述多元函数求偏导,令其为 \(0\) 有
\[\frac{\partial F}{\partial a_k}=2\sum_{i=0}^{s-1}\left[f(t_i)-\sum_{j=0}^{n-1}a_j\phi_j(t_i)\right][-\phi_k(t_i)]=0\qquad(k=0,1,\cdots,n-1),\]
整理为
\[\sum_{j=0}^{n-1}\left[\sum_{i=0}^{s-1}\phi_k(t_i)\phi_j(t_i)\right]a_j=\sum_{i=0}^{s-1}\phi_k(t_i)f(t_i)\qquad(k=0,1,\cdots,n-1)\tag{4-3}\]
不同的 2 个数字向量的内积定义为 \((\pmb\alpha,\pmb\beta)=\sum\limits_{i=0}^sa_ib_i\),同样的,多项式不同的 2 个分量(例如 \(\phi_1(t)=t\) 和 \(\phi_2(t)=t^2\) 就是不同的分量)之间的内积可以定义为 \((\phi_p(t),\phi_q(t))=\sum\limits_{i=0}^{s-1}\phi_p(t_i)\phi_q(t_i)\),简记为 \((\phi_p,\phi_q)\)。则有
\[\left\{\begin{align} (\phi_k,\phi_j)&=\sum_{i=0}^{s-1}\phi_k(t_i)\phi_j(t_i)\\ (\phi_k,f)&=\sum_{i=0}^{s-1}\phi_k(t_i)f(t_i)\equiv d_k\\ \end{align}\right.\tag{4-4}\]
于是公式 \(\text{(4-3)}\) 可以写成
\[\sum_{j=0}^{n-1}(\phi_k,\phi_j)=d_k\qquad(k=0,1,\cdots,n-1)\tag{4-5a}\]
或者展开写为
\[\left\{\begin{matrix} (\phi_0,\phi_0)a_0&+&(\phi_0,\phi_1)a_1&+&\cdots&+&(\phi_0,\phi_{n-1})a_{n-1}&=&d_0\\ (\phi_1,\phi_0)a_0&+&(\phi_1,\phi_1)a_1&+&\cdots&+&(\phi_1,\phi_{n-1})a_{n-1}&=&d_1\\ \vdots&&\vdots&&&&\vdots&=&\vdots\\ (\phi_{n-1},\phi_0)a_0&+&(\phi_{n-1},\phi_1)a_1&+&\cdots&+&(\phi_{n-1},\phi_{n-1})a_{n-1}&=&d_{n-1}\\ \end{matrix}\right.\tag{4-5b}\]
上式称为 \(a_0,a_1,\cdots,a_{n-1}\) 的法方程(组),是 \(n\) 阶线性方程组,其系数矩阵是
\[G=\begin{bmatrix} (\phi_0,\phi_0)&(\phi_0,\phi_1)&\cdots&(\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0)&(\phi_1,\phi_1)&\cdots&(\phi_1,\phi_{n-1})\\ \vdots&\vdots&&\vdots\\ (\phi_{n-1},\phi_0)&(\phi_{n-1},\phi_1)&\cdots&(\phi_{n-1},\phi_{n-1})\\ \end{bmatrix}\tag{4-6}\]
对于 \((\phi_p,\phi_q)\),可以写成矩阵的表示方式,即
\[\begin{align}(\phi_p,\phi_q)&=\sum_{i=0}^{s-1}\phi_p(t_i)\phi_q(t_i)\\&=[\phi_p(t_0),\phi_p(t_1),\cdots,\phi_p(t_{s-1})] \begin{bmatrix}\phi_i(t_0)\\\phi_i(t_1)\\\vdots\\\phi_q(t_{s-1})\end{bmatrix}\end{align}\tag{4-7}\]
因此对法方程系数矩阵 \(G\) 的第 \(k\ (k=0,1,\cdots,n-1)\) 行,有
\[[(\phi_k,\phi_0),(\phi_k,\phi_1),\cdots,(\phi_k,\phi_{n-1})]=[\phi_k(t_0),\phi_k(t_1),\cdots,\phi_k(t_{s-1})] \begin{bmatrix}\phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\\phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\\vdots&\vdots &&\vdots\\\phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1})\end{bmatrix}\tag{4-8}\]
将 \(k=0,1,\cdots,n-1\) 的行向量拼起来,得到
\[\begin{align}G&=\begin{bmatrix} (\phi_0,\phi_0)&(\phi_0,\phi_1)&\cdots&(\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0)&(\phi_1,\phi_1)&\cdots&(\phi_1,\phi_{n-1})\\ \vdots&\vdots&&\vdots\\ (\phi_{n-1},\phi_0)&(\phi_{n-1},\phi_1)&\cdots&(\phi_{n-1},\phi_{n-1})\\ \end{bmatrix}\\&=\begin{bmatrix} \phi_0(t_0)&\phi_0(t_1)&\cdots&\phi_0(t_{s-1})\\ \phi_1(t_0)&\phi_1(t_1)&\cdots&\phi_1(t_{s-1})\\ \vdots&\vdots&&\vdots\\ \phi_{n-1}(t_0)&\phi_{n-1}(t_1)&\cdots&\phi_{n-1}(t_{s-1})\\ \end{bmatrix}\begin{bmatrix} \phi_0(t_0)&\phi_1(t_0)&\cdots&\phi_{n-1}(t_0)\\ \phi_0(t_1)&\phi_1(t_1)&\cdots&\phi_{n-1}(t_1)\\ \vdots&\vdots&&\vdots\\ \phi_0(t_{s-1})&\phi_1(t_{s-1})&\cdots&\phi_{n-1}(t_{s-1}) \end{bmatrix}\end{align}\tag{4-9}\]
将公式 \(\text{(3-11)}\) 中 \(A\) 的矩阵表示方式代入 \(\text{(4-9)}\) 可以得到 \(G=A^TA\),并且右端项 \(\pmb d=A^T\pmb f\),代入公式 \(\text{(4-5)}\) 可以得到
\[A^TA\pmb a=A^T\pmb f\tag{4-10}\]
即
\[\boxed{\hat{\pmb a}=\left(A^TA\right)^{-1}A^T\pmb f}\tag{4-11}\]
这与公式 \(\text{(2-7)}\) 完全一致。
对于示例 3,可以依次计算出
\[\begin{align} (\phi_0,\phi_0)&=\sum_{i=0}^3\phi_0(t_i)\phi_0(t_i)=\sum_{i=0}^31\times1=4\\ (\phi_1,\phi_0)=(\phi_0,\phi_1)&=\sum_{i=0}^3\phi_0(t_i)\phi_1(t_i)=\sum_{i=0}^31\times t_i=1+2+3+4=10\\ (\phi_1,\phi_1)&=\sum_{i=0}^3\phi_1(t_i)\phi_1(t_i)=\sum_{i=0}^3t_i\times t_i=1+4+9+16=30\\ d_0=(\phi_0,f)&=\sum_{i=0}^3\phi_0(t_i)f(t_i)=\sum_{i=0}^31\times f(t_i)=0+2+1+3=6\\ d_1=(\phi_1,f)&=\sum_{i=0}^3\phi_1(t_i)f(t_i)=\sum_{i=0}^3t_i\times f(t_i)=0+2\times2+3\times1+4\times3=19\\ \end{align}\tag{4-12}\]
得到
\[\begin{bmatrix}4&10\\10&30\end{bmatrix}\hat{\pmb a}= \begin{bmatrix}6\\19\end{bmatrix}\tag{4-13}\]
解得: \(\left\{\begin{align}a_0&=-0.5\\a_1&=0.8\end{align}\right.\),即拟合曲线为 \(y=-0.5+0.8t\),使用数学绘图软件验证,结果正确。
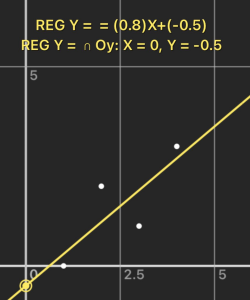
OpenCV 中提供了最小二乘法求解的函数 cv::solve(),并设置有 2 个相关的成员函数,其函数原型如下。此外可参考 cv::solve 的 OpenCV 手册。
有关递推最小二乘法的介绍可参考 k 步前向预估神符预测 。
 1.9.1
1.9.1