 |
RMVL
1.4.0
Robotic Manipulation and Vision Library
|
 |
RMVL
1.4.0
Robotic Manipulation and Vision Library
|
包含最速下降、共轭梯度的介绍
上一篇教程:一维最优化方法 ↑
下一篇教程:基于 TOPSIS 模型的熵权法 ↓
\[ \def\red#1{\color{red}{#1}} \def\teal#1{\color{teal}{#1}} \def\green#1{\color{green}{#1}} \def\transparent#1{\color{transparent}{#1}} \def\orange#1{\color{orange}{#1}} \def\fml#1{\text{(#1)}} \]
沿函数的负梯度方向,函数值下降最多,因此,对于存在导数的连续目标函数,最速下降法是一种简单而有效的优化方法。可以将目标函数的负梯度方向作为寻优方向,即
\[\pmb s_k=-\frac{\nabla f(\pmb x_k)}{\|\nabla f(\pmb x_k)\|}\tag{1-1}\]
因此当前点为 \(\pmb x_k\) 时,下一个点的表达式为
\[\pmb x_{k+1}=\pmb x_k+\alpha_k\pmb s_k=\pmb x_k-\alpha_k\frac{\nabla f(\pmb x_k)}{\|\nabla f(\pmb x_k)\|}\tag{1-2}\]
对于每轮得到的一个新的负梯度方向,再利用 一维最优化方法 求解 \(\alpha_k\)。最速下降法的迭代步骤如下:
\[f(\pmb x_k+\alpha_k\pmb s_k)=\min_{\alpha>0}f(\pmb x_k+\alpha\pmb s_k)\tag{1-3}\]
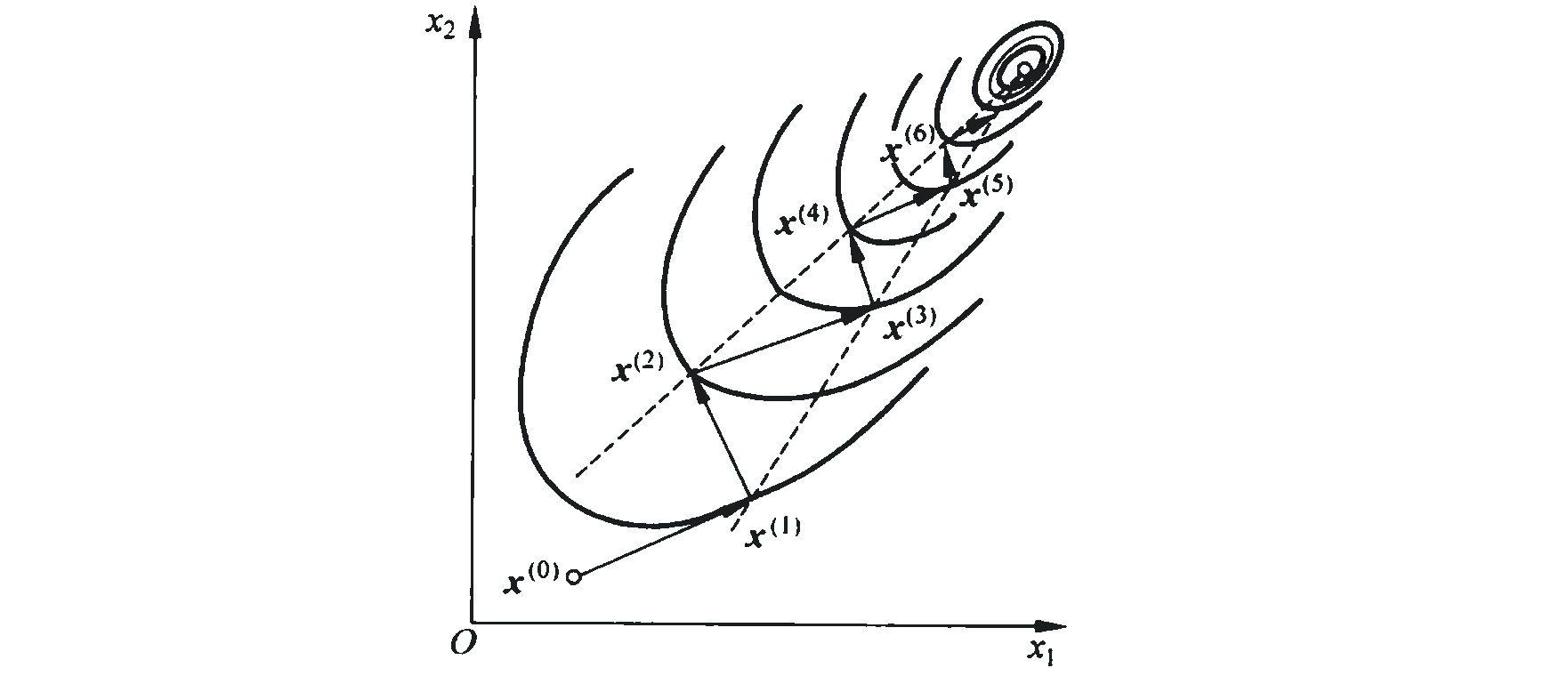
最速下降法对于一般的函数而言,在远离极值点时函数值下降得很快,最速下降法队椭圆类函数十分有效,可以很快搜索到接近极值点。但是当距离极值点较近时,特别是存在脊线的目标函数,收敛过程可能会十分缓慢,如图 1-1 所示。
同心椭圆族曲线的两平行切线有这样的特性:通过两平行线与椭圆的切点作连线,该直线通过该椭圆族的中心,如图 2-1 所示。因为该连线的方向与两平行线是共轭方向,所以利用这一特性寻优称为共轭方向法。

如果有一组 \(n\) 个非零向量组 \(\pmb s_1,\pmb s_2,\dots,\pmb s_n\in\pmb E^n\),且这个向量组中的任意两个向量关于 \(n\) 阶实对称正定矩阵 \(\pmb A\) 满足式
\[\pmb s_i^T\pmb A\pmb s_j=0,\quad i,j=1,2,\dots,n\ 且\ i\ne j\tag{2-1}\]
则称
有这一个特殊情况,当矩阵 \(\pmb A\) 是单位矩阵时,向量的共轭就相当于向量的正交。共轭方向相当于将原来的非正椭圆函数通过矩阵 \(\pmb A\) 变换为正圆函数,而共轭方向 \(\pmb s_1\) 和 \(\pmb s_2\) 则是变换后的垂直方向 \(\pmb p_1\) 和 \(\pmb p_2\),如图 2-2 所示。

在极值点 \(x^*\) 附近,目标函数可以近似为二次型函数,即
\[f(\pmb x)\approx c+\pmb b^T\pmb x+\frac12\pmb x^T\pmb A\pmb x\tag{2-2}\]
\[\pmb s_{k+1}=-\nabla f(\pmb x_{k+1})+\beta_k\pmb s_k\tag{2-3}\]
在公式 \(\fml{2-3}\) 中, \(\beta_k\) 按下式计算时,可满足共轭条件 \(\pmb s_{k+1}^T\pmb A\pmb s_k=0\):\[\beta_k=\frac{\|\nabla f(\pmb x_{k+1})\|^2}{\|\nabla f(\pmb x_k)\|^2}\tag{2-4}\]
上面只是对目标函数为二次型函数的情况求得了构成共轭方向的系数 \(\beta_k\),对于一般的目标函数,有
\[\beta_k=\frac{\|\nabla f(\pmb x_{k+1})\|^2-[\nabla f(\pmb x_{k+1})]^T\nabla f(\pmb x_k)}{\|\nabla f(\pmb x_k)\|^2}\tag{2-5}\]
从而类似式 \(\fml{2-3}\) 有
\[\pmb s_{k+1}=-\nabla f(\pmb x_{k+1})+\beta_k\pmb s_k\]
\[\pmb s_{k+1}=-\nabla f(\pmb x_{k+1})+\beta_k\pmb s_k\]
首先定义一个目标函数,例如:
然后调用 rm::fminunc 函数:
汇总起来,共轭梯度法的使用实例如下:
运行结果如下:
 1.12.0
1.12.0